Question

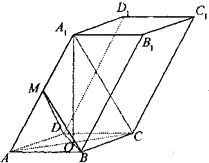已知四棱柱ABCD-A₁B₁C₁D₁的底面ABCD是边长为2的菱形，AC∩BD=O，AA₁=2

3

，BD⊥A₁A，∠BAD=∠A₁AC=60°，点M是棱AA₁的中点．
（Ⅰ）求证：A₁C∥平面BMD；
（Ⅱ）求证：A₁O⊥平面ABCD；
（Ⅲ）求直线BM与平面BC₁D所成角的正弦值．

Answer 1

考点：直线与平面所成的角,直线与平面平行的判定,直线与平面垂直的判定

专题：空间角

分析：（Ⅰ）连结MO，由已知条件推导出MO∥A₁C，由此能证明A₁C∥平面BMD．
（Ⅱ）由已知条件推导出BD⊥面A₁AC，AO=

1

2

AC=

3

，由此能证明A₁O⊥平面ABCD．
（Ⅲ）以O为原点，以OA为x轴，OB为y轴，OA₁为z轴，建立直角坐标系，利用向量法能求出直线BM与平面BC₁D所成角的正弦值．

解答： （Ⅰ）证明：连结MO，
∵A₁M=MA，AO=OC，
∴MO∥A₁C，
∵MO?平面BMD，A₁C不包含于平面BMD，
∴A₁C∥平面BMD．…（3分）
（Ⅱ）证明：∵BD⊥AA₁，BD⊥AC，∴BD⊥面A₁AC，
于是BD⊥A₁O，AC∩BD=O，
∵AB=CD=2，∠BAD=60°，
∴AO=

1

2

AC=

3

，
又∵AA₁=2

3

，∠A₁AC=60°，∴A₁O⊥AC，
又∵A₁O⊥BD，∴A₁O⊥平面ABCD．…（7分）
（Ⅲ）解：如图，以O为原点，以OA为x轴，OB为y轴，OA₁为z轴，建立直角坐标系，
由题意知A1(0，0，3)，A(

3

，0，0)，C（-

3

，0，0），B（0，1，0），D（0，-1，0），
∵

A1C1

=

AC

=(-2

3

，0，0)，∴C1=(-2

3

，0，3)，
∵M（

3

2

，0，

3

2

），∴

MB

=（-

3

2

，1，-

3

2

），

DB

=(0，2，0)，

BC1

=（-2

3

，-1，3），
设平面BC₁D的法向量为

n

=（x，y，z），
则

n • DB =2y=0 n • BC1 =-2 3 x-y+3z=0

，
取x=

3

，得

n

=(

3

，0，2)，…（9分）
∴cos＜

MB

，

n

＞=

- 3 2 -3

2 7

=-

9

4 7

，…（11分）
∴直线BM与平面BC₁D所成角的正弦值为

9 7

28

．…（12分）

点评：本题考查直线与平面平行的证明，考查直线与平面平行的证明，考查直线与平面所成角的正弦值的求法，解题时要注意向量法的合理运用．