题目内容
化简或求值:(1)sin2α+sin2β-sin2αsin2β+cos2αcos2β
(2)
.
(2)
| 1-2sin40°cos40° |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)原式2、4项结合提取公因式后,利用同角三角函数间的基本关系化简,再结合,提取公因式后,利用同角三角函数间的基本关系化简,即可得到结果;
(2)原式被开方数“1”变形后,利用完全平方公式化简,再利用二次根式的化简公式计算即可得到结果.
(2)原式被开方数“1”变形后,利用完全平方公式化简,再利用二次根式的化简公式计算即可得到结果.
解答:
解:(1)原式=sin2α+sin2β(1-sin2α)+cos2αcos2β
=sin2α+(sin2βcos2α+cos2αcos2β)
=sin2α+cos2α(sin2β+cos2β)
=sin2α+cos2α
=1;
(2)∵sin40°-cos40°<0,
∴原式=
=
=|sin40°-cos40°|
=cos40°-sin40°.
=sin2α+(sin2βcos2α+cos2αcos2β)
=sin2α+cos2α(sin2β+cos2β)
=sin2α+cos2α
=1;
(2)∵sin40°-cos40°<0,
∴原式=
| sin240°+cos240°-2sin40°cos40° |
=
| (sin40°-cos40°)2 |
=|sin40°-cos40°|
=cos40°-sin40°.
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
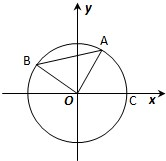 如图,A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴的交点,△AOB为正三角形.若A点的坐标为(x,y).记∠COA=α,求|BC|2的取值范围.
如图,A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴的交点,△AOB为正三角形.若A点的坐标为(x,y).记∠COA=α,求|BC|2的取值范围. 如图,一半径为
如图,一半径为