题目内容
有19人围成一圈,从中选出4个人,要求这4个人恰好有3人相邻,一共有 种不同的选法.
考点:排列、组合的实际应用
专题:应用题,排列组合
分析:第一步:19个人围成一圈,要从中取出3个相邻的人;第二步:若从已取出任意的三个人,还剩下的有16个人,因为第四人不与已取出的三人相邻,所以再去除左右相邻的两人,根据乘法原理可得不同的选法.
解答:
解:第一步:19个人围成一圈,要从中取出3个相邻的人,有19种取法;
第二步:若从已取出任意的三个人,还剩下的有16个人,因为第四人不与已取出的三人相邻,所以再去除左右相邻的两人,为14人,
所以根据乘法原理可得,共有19×(19-3-2)=19×14=266(种).
故答案为:266.
第二步:若从已取出任意的三个人,还剩下的有16个人,因为第四人不与已取出的三人相邻,所以再去除左右相邻的两人,为14人,
所以根据乘法原理可得,共有19×(19-3-2)=19×14=266(种).
故答案为:266.
点评:本题考查了利用“捆绑法”处理一些较复杂的排列组合问题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
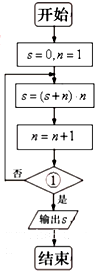
如图是某算法的程序框图,则程序运行后输出的结果是124,则判断框①处应填入的条件是( )

| A、n>2 | B、n>3 |
| C、n>4 | D、n>5 |