题目内容
一工厂有A，B两台独立工作的机器，平均来说，每个机器24小时发生故障一次，若修复机器A需要一小时，修复机器B需要2小时，试求生产在24小时内被中断的概率．（假定故障发生时间可落在这段时间内的任一时刻）
考点：相互独立事件的概率乘法公式
专题：概率与统计
分析：根据概率求出A，B正常的概率，根据概率公式即可得到结论．
解答：
解：A发生故障的概率为
，B发生故障的概率为
=
．
若要生产不终断AB需同时正常，A正常1-
=
，B正常，1-
=
，
则生产不被中断为
×
，
则生产被中断为1-
×
=
=
=0.121
| 1 |
| 24 |
| 2 |
| 24 |
| 1 |
| 12 |
若要生产不终断AB需同时正常，A正常1-
| 1 |
| 24 |
| 23 |
| 24 |
| 1 |
| 12 |
| 11 |
| 12 |
则生产不被中断为
| 23 |
| 24 |
| 11 |
| 12 |
则生产被中断为1-
| 23 |
| 24 |
| 11 |
| 12 |
| 288-253 |
| 288 |
| 35 |
| 288 |
点评：本题主要考查概率的计算，求出A，B正确的概率是解决本题的关键．
练习册系列答案
相关题目
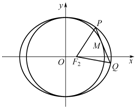已知椭圆
如图，焦点在x轴上的椭圆T1与焦点在y轴上的椭圆T2相切于点M（0，1），且椭圆T1与T2的离心率均为
如图，在Rt△ABC中，∠BAC、∠ABC、∠ACB成等差数列，且AB=4，D点是斜边BC上一动点，连接AD，以AD为折痕，将△ABD折到与△ADC的同一个平面内，B变为B1，设∠BAD=θ．