题目内容
已知点P是以F1，F2为焦点的双曲线
-
=1（a＞0，b＞0）上一点，
•
=0，tan∠PF1F2=
，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| 1 |
| 2 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据双曲线的定义可知|PF1|-|PF2|=2a，进而根据tan∠PF1F2=
，可得|PF1|=2|PF2|，分别求得|PF2|和|PF1|，进而根据勾股定理建立等式求得a和c的关系，则离心率可得．
| 1 |
| 2 |
解答：
解：∵
•
=0，
∴PF1⊥PF2，
∵tan∠PF1F2=
，
∴|PF1|=2|PF2|
∵|PF1|-|PF2|=2a，
∴|PF2|=2a，|PF1|=4a；
在RT△PF1F2中，|F1F2|2=|PF1|2+|PF2|2，
∴4c2=4a2+16a2，解得e=
．
故选：C．
| PF1 |
| PF2 |
∴PF1⊥PF2，
∵tan∠PF1F2=
| 1 |
| 2 |
∴|PF1|=2|PF2|
∵|PF1|-|PF2|=2a，
∴|PF2|=2a，|PF1|=4a；
在RT△PF1F2中，|F1F2|2=|PF1|2+|PF2|2，
∴4c2=4a2+16a2，解得e=
| 5 |
故选：C．
点评：本题主要考查了双曲线的应用．考查了学生对双曲线定义和基本知识的掌握．
练习册系列答案
华东师大版一课一练系列答案
相关题目
已知实数x，y满足：
，则2x+y的取值范围为（ ）
|
A、[-
| ||||
B、[-2，
| ||||
| C、[-1，2] | ||||
| D、[-2，2] |
定义一种运算符号“?”，两个实数a，b的“a?b”运算原理如图所示，若输人a=2cos在复平面内，复数
对应的点位于（ ）
| 2i |
| 2+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
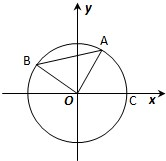如图，A，B是单位圆O上的动点，且A，B分别在第一，二象限．C是圆与x轴的交点，△AOB为正三角形．若A点的坐标为（x，y）．记∠COA=α，求|BC|2的取值范围．
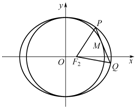已知椭圆