Question

如图所示，已知椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的右焦点为F₂（1，0），点A（1，

3

2

）在椭圆上．
（1）求椭圆方程；
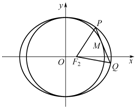
（2）点M（x₀，y₀）在圆x²+y²=b²上，点M在第一象限，过点M作圆x²+y²=b²的切线交椭圆于P、Q两点，问|

F2P

|+|

F2Q

|+|

PQ

|是否为定值？如果是，求出该定值；如果不是，说明理由．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：计算题,圆锥曲线的定义、性质与方程

分析：（I）由已知中椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的右焦点为F₂（1，0），可得c值，点H（1，

3

2

）在椭圆上，可得a值，进而求出b值后，可得椭圆方程；
（II）设P（x₁，y₁），Q（x₂，y₂），分别求出|F₂P|，|F₂Q|，结合相切的条件可得|PM|²=|OP|²-|OM|²求出|PQ|，可得结论．

解答： 解：（1）∵右焦点为F₂（1，0），∴c=1
∴左焦点为F₁（1，0），点H（1，

3

2

）在椭圆上，
∴2a=|HF₁|+|HF₂|=4，
∴a=2，
∴b=

a2-c2

=

3

∴椭圆方程为

x2

4

+

y2

3

=1----------------（5分）
（2）设P（x₁，y₁），Q（x₂，y₂），

x12

4

+

y12

3

=1（|x₁|≤2）
∴|PF₂|²=（x₁-1）²+y₁²=

1

4

（x₁-4）²，
∴|PF₂|=2-

1

2

x₁，------------------------（8分）
连接OM，OP，由相切条件知：
|PM|²=|OP|²-|OM|²=x₁²+y₁²-3=

1

4

x₁²，
∴|PM|=

1

2

x₁，
∴|PF₂|+|PM|=2----------------------------------（11分）
同理可求|QF₂|+|QM|=2
∴|F₂P|+|F₂Q|+|PQ|=4为定值．-------------（13分）

点评：本题考查的知识点是椭圆的标准方程，直线与圆的位置关系，直线与椭圆的位置关系，熟练掌握椭圆的性质是解答本题的关键．