题目内容
设x1,x2∈R,常数a>0,定义运算“*”为:x1*x2=4x1x2,等号右边是通常的乘法运算,如果在平面直角坐标系中,动点P的坐标(x,y)满足关系式:
*
=a*x,则动点P的轨迹方程为( )
| y |
| 2 |
| y |
| 2 |
A、y2=
| ||
| B、y2=ax | ||
| C、y2=2ax | ||
| D、y2=4ax |
考点:轨迹方程
专题:计算题,新定义,圆锥曲线的定义、性质与方程
分析:由于x1*x2=4x1x2,则
*
=a*x,即为4•
•
=4ax,即可得到答案.
| y |
| 2 |
| y |
| 2 |
| y |
| 2 |
| y |
| 2 |
解答:
解:由于x1*x2=4x1x2,
则
*
=a*x,即为4•
•
=4ax,
即有y2=4ax,
故选:D.
则
| y |
| 2 |
| y |
| 2 |
| y |
| 2 |
| y |
| 2 |
即有y2=4ax,
故选:D.
点评:本题考查新定义的理解和运用,考查运算能力,理解新定义是迅速解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
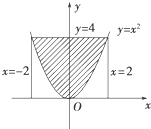 如图在区域Ω={(x,y)|-2≤x≤2,0≤y≤4}中随机撒豆子,豆子落在图中阴影部分内的概率为
如图在区域Ω={(x,y)|-2≤x≤2,0≤y≤4}中随机撒豆子,豆子落在图中阴影部分内的概率为