题目内容
有如下命题：已知椭圆
+
=1，AA′是椭圆的长轴，P（x1，y1）是椭圆上异于A，A′的任意一点，过P作斜率为-
的直线l，过直线l上的两点M，M′分别作x轴的垂线，垂足分别为点A，A′，则
（1）|AM||A′M′|为定值4；
（2）由A，A′，M′，M四点构成的四边形面积的最小值为12．
请分析上述命题，并根据上述命题对于椭圆
+
=1（a＞b＞0）构造出一个具有一般性结论的命题，使上述命题是一个特例，写出这一命题，并证明这一命题是真命题．
| x2 |
| 9 |
| y2 |
| 4 |
| 4x1 |
| 9y1 |
（1）|AM||A′M′|为定值4；
（2）由A，A′，M′，M四点构成的四边形面积的最小值为12．
请分析上述命题，并根据上述命题对于椭圆
| x2 |
| a2 |
| y2 |
| b2 |
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：分析题设命题，根据命题对于椭圆
+
=1（a＞b＞0）性质能构造出一个具有一般性结论的命题，使题设命题是一个特例，写出这一命题并证明：（1）不妨设A（-a，0），A′（a，0），则直线l：y-y1=-
(x-x1)，即b2x1x+a2y1y=b2x12+a2y12=a2b2，由M与A，M′与A′在相同的横坐标，能证明|AM||A′M′|=b2；（2）由题意知，不论四点的位置如何，四边形的面积S=
|AA′|(|AM|+|A′M′|)．由此能证明四边形的面积的最小值为2ab．
| x2 |
| a2 |
| y2 |
| b2 |
| b2x1 |
| a2y1 |
| 1 |
| 2 |
解答：
解：这一命题是：已知
+
=1，a＞b＞0，AA′是椭圆的长轴，P（x1，y1）是椭圆上异于A，A′的任意一点，过P作斜率为-
的直线l，过直线l上的两点M，M′分别作x轴的垂线，垂足分别为A，A′，则：
（1）|AM||A′M′|为定值b2；
（2）由A，A′，M′，M四点构成的四边形面积的最小值为2ab．（6分）．
这个命题是真命题，证明如下：
（1）不妨设A（-a，0），A′（a，0），则直线l：y-y1=-
(x-x1)，
即b2x1x+a2y1y=b2x12+a2y12=a2b2，
由M与A，M′与A′在相同的横坐标，
得M（-a，
），M′(a，
)，
∴|AM||A′M′|=|yMyM′|
=|
•
|
=|b2•
|=b2．（10分）
（2）由题意知，不论四点的位置如何，
四边形的面积S=
|AA′|(|AM|+|A′M′|)．
∵|AA'|=2a，且|AM|，|A′M′|都为正数，
∴S=
|AA′|(|AM|+|A′M′|)=a(|AM|+|A′M′|)≥a(2
)=2ab．
即四边形的面积的最小值为2ab．（14分）
| x2 |
| a2 |
| y2 |
| b2 |
| b2x1 |
| a2y1 |
（1）|AM||A′M′|为定值b2；
（2）由A，A′，M′，M四点构成的四边形面积的最小值为2ab．（6分）．
这个命题是真命题，证明如下：
（1）不妨设A（-a，0），A′（a，0），则直线l：y-y1=-
| b2x1 |
| a2y1 |
即b2x1x+a2y1y=b2x12+a2y12=a2b2，
由M与A，M′与A′在相同的横坐标，
得M（-a，
| ab2+b2x1 |
| ay1 |
| ab2-b2x1 |
| ay1 |
∴|AM||A′M′|=|yMyM′|
=|
| ab2+b2x1 |
| ay1 |
| ab2-b2x1 |
| ay1 |
=|b2•
| a2b2-b2x12 |
| a2y12 |
（2）由题意知，不论四点的位置如何，
四边形的面积S=
| 1 |
| 2 |
∵|AA'|=2a，且|AM|，|A′M′|都为正数，
∴S=
| 1 |
| 2 |
| |AM||A′M′| |
即四边形的面积的最小值为2ab．（14分）
点评：本题考查命题的叙述与证明，考查椭圆的性质、直线与圆锥曲线的关系、考查函数与方程思想、考查推理论证能力的培养，是中档题．
练习册系列答案
相关题目
设x1，x2∈R，常数a＞0，定义运算“*”为：x1*x2=4x1x2，等号右边是通常的乘法运算，如果在平面直角坐标系中，动点P的坐标（x，y）满足关系式：
*
=a*x，则动点P的轨迹方程为（ ）
| y |
| 2 |
| y |
| 2 |
A、y2=
| ||
| B、y2=ax | ||
| C、y2=2ax | ||
| D、y2=4ax |
函数f（x）=
ln
的图象可能是（ ）
| 1 |
| 3 |
| 1+x |
| 1-x |
A、 |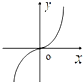
B、 |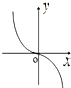
C、 |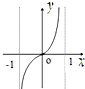
D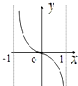、 |