题目内容
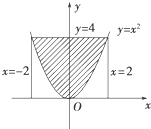如图在区域Ω={（x，y）|-2≤x≤2，0≤y≤4}中随机撒豆子，豆子落在图中阴影部分内的概率为考点：几何概型
专题：导数的综合应用,概率与统计
分析：先求构成试验的全部区域为圆内的区域的面积，再利用积分知识可得正弦曲线y=sinx与x轴围成的区域的面积，从而可求概率．
解答：
解：构成试验的全部区域为圆内的区域，面积为16．
正弦曲线y=x2与x轴围成的区域记为M，
根据图形的对称性得：面积为S=2∫02x2dx=2×
x3|02=
，
由几何概率的计算公式可得，随机往圆O内投一个点A，则点A落在区域M内的概率P=
=
．
故答案为：
．
正弦曲线y=x2与x轴围成的区域记为M，
根据图形的对称性得：面积为S=2∫02x2dx=2×
| 1 |
| 3 |
| 16 |
| 3 |
由几何概率的计算公式可得，随机往圆O内投一个点A，则点A落在区域M内的概率P=
16-
| ||
| 16 |
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：本题考查利用积分求解曲面的面积，几何概型的计算公式的运用，考查学生的计算能力，属于中档题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
设x1，x2∈R，常数a＞0，定义运算“*”为：x1*x2=4x1x2，等号右边是通常的乘法运算，如果在平面直角坐标系中，动点P的坐标（x，y）满足关系式：
*
=a*x，则动点P的轨迹方程为（ ）
| y |
| 2 |
| y |
| 2 |
A、y2=
| ||
| B、y2=ax | ||
| C、y2=2ax | ||
| D、y2=4ax |
函数f（x）=
ln
的图象可能是（ ）
| 1 |
| 3 |
| 1+x |
| 1-x |
A、 |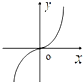
B、 |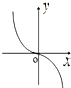
C、 |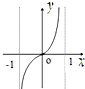
D、 |
已知A是三角形ABC的内角，则“sinA=
”是“cosA=
”的（ ）
| ||
| 2 |
| 1 |
| 2 |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |