题目内容
已知数列{an}为等比数列.
(1)若a1+a2+a3=21,a1a2a3=216,求an;
(2)若a3a5=18,a4a8=72,求公比q.
(1)若a1+a2+a3=21,a1a2a3=216,求an;
(2)若a3a5=18,a4a8=72,求公比q.
考点:等比数列的性质
专题:等差数列与等比数列
分析:(1)由等比数列的性质可得a23=216,可得a2=6,结合条件可得a1+a3=15.由未定定理可得a1,a3是方程x2-15x+36=0的两根,解方程可得a1的值,可得q,可得所求;(2)由题意可得18q4=72,解方程可得.
解答:
解:(1)由等比数列的性质可得a1a2a3=a23=216,∴a2=6,
∴a1a3=36且a1+a3=21-a2=15.
∴a1,a3是方程x2-15x+36=0的两根,
解方程可得两根为3和12.
当a1=3时,q=
=2,
∴an=3×2n-1;
同理,当a1=12时,q=
,an=12•(
)n-1=3×23-n.
(2)由题意可得a4a8=a3q•a5q3=a3a5q4=18q4=72,
∴q4=4,∴公比q=±
.
∴a1a3=36且a1+a3=21-a2=15.
∴a1,a3是方程x2-15x+36=0的两根,
解方程可得两根为3和12.
当a1=3时,q=
| a2 |
| a1 |
∴an=3×2n-1;
同理,当a1=12时,q=
| 1 |
| 2 |
| 1 |
| 2 |
(2)由题意可得a4a8=a3q•a5q3=a3a5q4=18q4=72,
∴q4=4,∴公比q=±
| 2 |
点评:本题考查等比数列的通项公式和性质,涉及分类讨论的思想,属中档题.

练习册系列答案
相关题目
函数f(x)=(sinx-cosx)•cosx的最小正周期为( )
| A、π | ||
B、
| ||
| C、2π | ||
D、
|
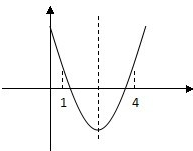 已知关于x不等式x2-2ax+a+2≤0(a∈R)的解集为M.
已知关于x不等式x2-2ax+a+2≤0(a∈R)的解集为M.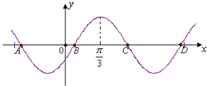 已知函数f(x)=sin(ωx+φ)(ω>0)的部分图象如图所示,点B(
已知函数f(x)=sin(ωx+φ)(ω>0)的部分图象如图所示,点B(