题目内容
已知圆C的圆心在坐标原点,且与直线l1:x-y-2
=0相切;
(1)求圆C的标准方程;
(2)过点(1,3)的直线与圆C交于A、B两点,且|AB|=2
,求此直线方程;
(3)若与直线l1垂直的直线l与圆C交于不同的B、D两点,且满足∠BOD为钝角,求直线l纵截距的取值范围?
| 2 |
(1)求圆C的标准方程;
(2)过点(1,3)的直线与圆C交于A、B两点,且|AB|=2
| 3 |
(3)若与直线l1垂直的直线l与圆C交于不同的B、D两点,且满足∠BOD为钝角,求直线l纵截距的取值范围?
考点:圆的标准方程,直线与圆的位置关系
专题:直线与圆
分析:(1)由圆心(0,0)到直线l1:x-y-2
=0距离为圆的半径,由已知条件能求出圆C的标准方程.
(2)圆心坐标为C(0,0),半径r=2,设直线方程y=k(x-1)+3,由圆心到直线的距离能求出满足条件的直线方程.
(3)设直线方程为y=-x+b,联立
,得2x2-2bx+b2-4=0,由此能求出直线l纵截距的取值范围.
| 2 |
(2)圆心坐标为C(0,0),半径r=2,设直线方程y=k(x-1)+3,由圆心到直线的距离能求出满足条件的直线方程.
(3)设直线方程为y=-x+b,联立
|
解答:
解:(1)根据题意:圆心(0,0)到直线l1:x-y-2
=0距离为圆的半径,
∴r=
=2,
∴圆C的标准方程为x2+y2=4.
(2)圆心坐标为C(0,0),半径r=2,
∵|AB|=2
,∴圆心到直线l的距离d=
=1,
当直线斜率存在,设为k,则直线方程y=k(x-1)+3,
即kx-y+3-k=0,
圆心到直线的距离为d=
=1,
解得k=
,
∴直线方程为y=
(x-1)+3,即4x-3y+5=0.
综上,满足条件的直线方程为4x-3y+5=0或x=1.
(3)设直线方程为y=-x+b,
联立
,得2x2-2bx+b2-4=0,
设直线l与圆的交点B(x1,y1),D(x2,y2),
由△=(-2b)2-8(b2-4)>0,得b2<8,
∴x1+x2=b,x1x2=
,①
∵∠BOD为钝角,∴
•
<0,即满足x1x2+y1y2<0,
且
与
不反向共线,
又y1=-x1+b,y2=-x2+b,
∴x1x2+y1y2=2x1x2-b(x1+x2)+b2<0,②
由①②得b2<4,满足△>0,即-2<b<2,
当
与
反向共线时,直线y=-x+b过原点,此时b=0,不满足题意,
∴直线l纵截距的取值范围是-2<b<2,且b≠0.
| 2 |
∴r=
2
| ||
|
∴圆C的标准方程为x2+y2=4.
(2)圆心坐标为C(0,0),半径r=2,
∵|AB|=2
| 3 |
| 4-3 |
当直线斜率存在,设为k,则直线方程y=k(x-1)+3,
即kx-y+3-k=0,
圆心到直线的距离为d=
| |3-k| | ||
|
解得k=
| 4 |
| 3 |
∴直线方程为y=
| 4 |
| 3 |
综上,满足条件的直线方程为4x-3y+5=0或x=1.
(3)设直线方程为y=-x+b,
联立
|
设直线l与圆的交点B(x1,y1),D(x2,y2),
由△=(-2b)2-8(b2-4)>0,得b2<8,
∴x1+x2=b,x1x2=
| b2-4 |
| 2 |
∵∠BOD为钝角,∴
| OB |
| OD |
且
| OB |
| OD |
又y1=-x1+b,y2=-x2+b,
∴x1x2+y1y2=2x1x2-b(x1+x2)+b2<0,②
由①②得b2<4,满足△>0,即-2<b<2,
当
| OB |
| OD |
反向共线时,直线y=-x+b过原点,此时b=0,不满足题意,
∴直线l纵截距的取值范围是-2<b<2,且b≠0.
点评:本题考查圆的方程的求法,考查直线方程的求法,考查直线的截距的取值范围的求法,解题时要认真审题,注意点到直线距离的合理运用.

练习册系列答案
相关题目
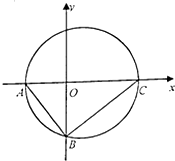 如图所示,在Rt△ABC中,已知A(-2,0),直角顶点B(0,-2
如图所示,在Rt△ABC中,已知A(-2,0),直角顶点B(0,-2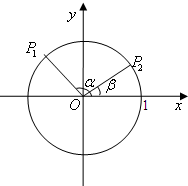 如图在单位圆中,已知α、β是坐标平面内的任意两个角,且0≤α-β≤π,
如图在单位圆中,已知α、β是坐标平面内的任意两个角,且0≤α-β≤π,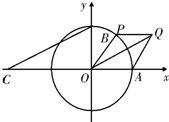 如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.
如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.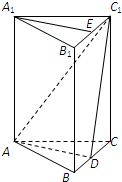 如图,在直三棱柱ABC-A1B1C1中,AB=AC,点D为BC中点,点E在线段B1C1上.
如图,在直三棱柱ABC-A1B1C1中,AB=AC,点D为BC中点,点E在线段B1C1上.