题目内容
已知二阶矩阵M有特征值λ=8及对应的一个特征向量
=
,并且矩阵M对应的变换将点(-1,2)变换成(-2,4).
(1)求矩阵M;
(2)求矩阵M的另一个特征值,及对应的一个特征向量
的坐标之间的关系;
(3)求直线l:2x-4y+1=0在矩阵M的作用下的直线l′的方程.
| e1 |
|
(1)求矩阵M;
(2)求矩阵M的另一个特征值,及对应的一个特征向量
| e2 |
(3)求直线l:2x-4y+1=0在矩阵M的作用下的直线l′的方程.
考点:矩阵特征值的定义,特征向量的定义
专题:选作题,矩阵和变换
分析:(1)先设矩阵M=
,这里a,b,c,d∈R,由二阶矩阵M有特征值λ=8及对应的一个特征向量
及矩阵M对应的变换将点(-1,2)换成(-2,4),得到关于a,b,c,d的方程组,即可求得矩阵M;
(2)由(1)知,矩阵M的特征多项式为f(λ)=(λ-6)(λ-4)-8=λ2-10λ+16,从而求得另一个特征值为2,设矩阵M的另一个特征向量是
=
,解得特征向量
=
的坐标之间的关系.
(3)设出点(x,y)是直线l上的任一点,其在矩阵M的变换下对应的点的坐标为(x′,y′),根据变换前后写出关系式,整理出要求的直线l′的方程.
|
| e1 |
(2)由(1)知,矩阵M的特征多项式为f(λ)=(λ-6)(λ-4)-8=λ2-10λ+16,从而求得另一个特征值为2,设矩阵M的另一个特征向量是
| e2 |
|
| e2 |
|
(3)设出点(x,y)是直线l上的任一点,其在矩阵M的变换下对应的点的坐标为(x′,y′),根据变换前后写出关系式,整理出要求的直线l′的方程.
解答:
解:(1)设矩阵M=
,这里a,b,c,d∈R,
则
=8
=
,故
①
=
,故
②
由①②联立解得
,∴M=
;
(2)由(1)知,矩阵M的特征多项式为f(λ)=λ2-10λ+16,故其另一个特征值为2,
设矩阵M的另一个特征向量是
=
,则
=2
,所以2x+y=0;
(3)设点(x,y)是直线l上任一点,其在矩阵M的变换下对应的点的坐标为(x′,y′),
则
=
,所以x=
x′-
y′,y=-
x′+
y′,
代入直线l的方程后,化简可得:x′-y′+2=0,即x-y+2=0.
∴直线l:x-y+1=0在矩阵M的作用下的直线l′的方程为x-y+2=0.
|
则
|
|
|
|
|
|
|
|
|
由①②联立解得
|
|
(2)由(1)知,矩阵M的特征多项式为f(λ)=λ2-10λ+16,故其另一个特征值为2,
设矩阵M的另一个特征向量是
| e2 |
|
|
|
|
(3)设点(x,y)是直线l上任一点,其在矩阵M的变换下对应的点的坐标为(x′,y′),
则
|
|
|
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 4 |
| 3 |
| 8 |
代入直线l的方程后,化简可得:x′-y′+2=0,即x-y+2=0.
∴直线l:x-y+1=0在矩阵M的作用下的直线l′的方程为x-y+2=0.
点评:本题主要考查了二阶矩阵,以及特征值与特征向量的计算,属于基础题.

练习册系列答案
相关题目
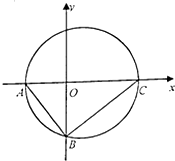 如图所示,在Rt△ABC中,已知A(-2,0),直角顶点B(0,-2
如图所示,在Rt△ABC中,已知A(-2,0),直角顶点B(0,-2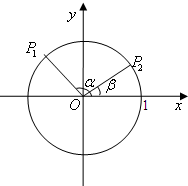 如图在单位圆中,已知α、β是坐标平面内的任意两个角,且0≤α-β≤π,
如图在单位圆中,已知α、β是坐标平面内的任意两个角,且0≤α-β≤π,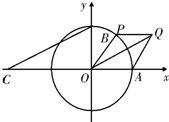 如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.
如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.