题目内容
已知函数f（x）=2sin（ωx+φ），x∈R（其中ω＞0，0＜φ＜
）的图象上一个点为M（
，-2），相邻两条对称轴之间的距离为
．
（1）求f（x）的解析式；
（2）当x∈[0，π]时，求f（x）的单调递增区间．
| π |
| 2 |
| 5π |
| 8 |
| π |
| 2 |
（1）求f（x）的解析式；
（2）当x∈[0，π]时，求f（x）的单调递增区间．
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,正弦函数的单调性
专题：三角函数的图像与性质
分析：（1）由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值．
（2）（2）由 2kπ-
≤2x+
≤2kπ+
求得 x的范围，可得f（x）的单调递增区间．再结合x∈[0，π]，可得结论．
（2）（2）由 2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
解答：
20．解：（1）相邻两条对称轴之间的距离为
，即T=π=
，∴ω=2．
根据 M（
，-2）在图象上得：2sin（2×
+φ）=-2，∴
+φ=2kπ+
，k∈z．
故φ=2kπ+
．
结合0＜φ＜
，可得φ=
，∴函数f（x）=2sin（2x+
）．
（2）由 2kπ-
≤2x+
≤2kπ+
得 kπ-
≤x≤kπ+
，k∈z，
故函数的增区间为[kπ-
，kπ+
]，k∈z．
再结合x∈[0，π]，可得增区间为[0，
]、[
，π]．
| π |
| 2 |
| 2π |
| ω |
根据 M（
| 5π |
| 8 |
| 5π |
| 8 |
| 5π |
| 4 |
| 3π |
| 2 |
故φ=2kπ+
| π |
| 4 |
结合0＜φ＜
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
（2）由 2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| π |
| 8 |
故函数的增区间为[kπ-
| 3π |
| 8 |
| π |
| 8 |
再结合x∈[0，π]，可得增区间为[0，
| π |
| 8 |
| 5π |
| 8 |
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，正弦函数的单调性，属于基础题．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
选修4.1：几何证明选讲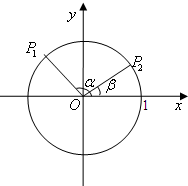
如图在单位圆中，已知α、β是坐标平面内的任意两个角，且0≤α-β≤π，
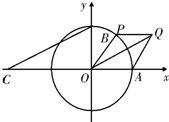如图所示，A，B分别是单位圆与x轴、y轴正半轴的交点，点P在单位圆上，∠AOP=θ（0＜θ＜π），C点坐标为（-2，0），平行四边形OAQP的面积为S．
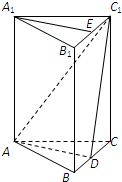如图，在直三棱柱ABC-A1B1C1中，AB=AC，点D为BC中点，点E在线段B1C1上．