题目内容
已知函数f(x)=log2(-4x+5•2x+1-16).
(1)求f(x)的定义域;
(2)求f(x)在区间[2,log27]上的值域.
(1)求f(x)的定义域;
(2)求f(x)在区间[2,log27]上的值域.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)根据函数f(x)的解析式可得-4x+5•2x+1-16>0,即(2x-2)(2x-8)<0,求得2x的范围,可得1x的范围,从而得到函数的定义域.
(2)根据x∈[2,log27],可得2x的范围,从而求得-(2x-2)(2x-8)的范围,由此求得f(x)的值域.
(2)根据x∈[2,log27],可得2x的范围,从而求得-(2x-2)(2x-8)的范围,由此求得f(x)的值域.
解答:
解:(1)∵函数f(x)=log2(-4x+5•2x+1-16)=log2[-(2x-2)(2x-8)],∴-4x+5•2x+1-16>0,
即(2x-2)(2x-8)<0,可得 2<2x<8,求得1<x<3,故函数的定义域为(1,3).
(2)∵x∈[2,log27],∴2x∈[4,7],∴-(2x-2)(2x-8)∈[5,9],
∴f(x)的值域为[log25,2log23].
即(2x-2)(2x-8)<0,可得 2<2x<8,求得1<x<3,故函数的定义域为(1,3).
(2)∵x∈[2,log27],∴2x∈[4,7],∴-(2x-2)(2x-8)∈[5,9],
∴f(x)的值域为[log25,2log23].
点评:本题主要考查对数函数的图象和性质综合应用,二次函数的性质,属于基础题.

练习册系列答案
相关题目
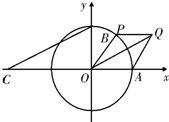 如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.
如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.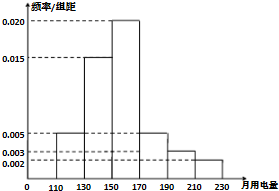 2013年第三季度,国家电网决定对城镇居民用电计费标准作出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图,如图所示.
2013年第三季度,国家电网决定对城镇居民用电计费标准作出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图,如图所示.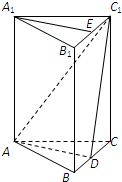 如图,在直三棱柱ABC-A1B1C1中,AB=AC,点D为BC中点,点E在线段B1C1上.
如图,在直三棱柱ABC-A1B1C1中,AB=AC,点D为BC中点,点E在线段B1C1上.