题目内容
(1)求函数f(x)=2x(5-3x),x∈(0,
)的最大值.
(2)已知x>0,y>0,且x+2y=1,求
+
的最小值.
| 5 |
| 3 |
(2)已知x>0,y>0,且x+2y=1,求
| 1 |
| x |
| 1 |
| y |
考点:基本不等式
专题:不等式的解法及应用
分析:(1)f(x)=2x•(5-3x)=
×3x(5-3x),根据基本不等式的性质,即可求出,注意等号成立的条件,
(2)灵活利用1=2x+y,化简
+
得,再根据基本不等式的性质,即可求出,注意等号成立的条件.
| 2 |
| 3 |
(2)灵活利用1=2x+y,化简
| 1 |
| x |
| 1 |
| y |
解答:
解:(1)∵x∈(0,
),
∴5-3x>0.
∴f(x)=2x•(5-3x)=
×3x(5-3x)≤
(
)2=
当且仅当3x=5-3x,即x=
时等号成立.
故f(x)的最大值为
.
(2)解:因为x>0,y>0,且x+2y=1,
所以
+
=
+
=3+
+
≥3+
=3+2
当且仅当且x+2y=1,即x=
-1,y=1-
时取得等号.
所以
+
的最小值为3+2
| 5 |
| 3 |
∴5-3x>0.
∴f(x)=2x•(5-3x)=
| 2 |
| 3 |
| 2 |
| 3 |
| 3x+5-3x |
| 2 |
| 25 |
| 6 |
当且仅当3x=5-3x,即x=
| 5 |
| 6 |
故f(x)的最大值为
| 4 |
| 6 |
(2)解:因为x>0,y>0,且x+2y=1,
所以
| 1 |
| x |
| 1 |
| y |
| x+2y |
| x |
| x+2y |
| y |
| 2y |
| x |
| x |
| y |
|
| 2 |
当且仅当且x+2y=1,即x=
| 2 |
| ||
| 2 |
所以
| 1 |
| x |
| 1 |
| y |
| 2 |
点评:本题主要考查了基本不等式的应用,关键是灵活构造符合基本不等式的形式,属于基础题.

练习册系列答案
相关题目
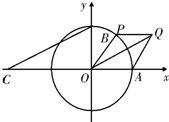 如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.
如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.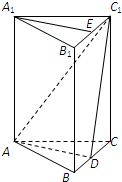 如图,在直三棱柱ABC-A1B1C1中,AB=AC,点D为BC中点,点E在线段B1C1上.
如图,在直三棱柱ABC-A1B1C1中,AB=AC,点D为BC中点,点E在线段B1C1上.