题目内容
(1)若实数x,y满足:
,求
的范围;
(2)设正数x,y满足x+2y=1,求
+
的最小值;
(3)已知x<
,求y=4x+
-2的最大值.
|
| y |
| x |
(2)设正数x,y满足x+2y=1,求
| 1 |
| x |
| 1 |
| y |
(3)已知x<
| 5 |
| 4 |
| 1 |
| 4x-5 |
考点:基本不等式
专题:不等式的解法及应用
分析:(1)根据不等式的性质可求
的范围;
(2)利用基本不等式的性质即可求
+
的最小值;
(3)利用基本不等式的性质求y=4x+
-2的最大值.
| y |
| x |
(2)利用基本不等式的性质即可求
| 1 |
| x |
| 1 |
| y |
(3)利用基本不等式的性质求y=4x+
| 1 |
| 4x-5 |
解答:
解:(1)由x-y+1≤0,即y≥x+1,
∵x>0,
∴
≥
=1+
>1,
即
的范围是(1,+∞).
(2)∵x+2y=1,
∴
+
=(x+2y)(
+
)=1+2+
+
≥3+2
=3+2
,
当且仅当
=
,即x=
y时取等号,
故
+
的最小值是3+2
.
(3)∵x<
,∴4x-5<0,
则y=4x+
-2=y=4x-5+
+3≤-2
+3=3-2=1,
故y=4x+
-2的最大值为1.
∵x>0,
∴
| y |
| x |
| x+1 |
| x |
| 1 |
| x |
即
| y |
| x |
(2)∵x+2y=1,
∴
| 1 |
| x |
| 1 |
| y |
| 1 |
| x |
| 1 |
| y |
| 2y |
| x |
| x |
| y |
|
| 2 |
当且仅当
| 2y |
| x |
| x |
| y |
| 2 |
故
| 1 |
| x |
| 1 |
| y |
| 2 |
(3)∵x<
| 5 |
| 4 |
则y=4x+
| 1 |
| 4x-5 |
| 1 |
| 4x-5 |
(5-4x)•
|
故y=4x+
| 1 |
| 4x-5 |
点评:本题主要考查不等式的应用,要求熟练掌握基本不等式的应用,注意不等式成立的条件.

练习册系列答案
相关题目
在△ABC中,内角A、B、C的对边分别是a、b、c,若b2-c2=
ac,sinA=2
sinC,则B=( )
| 3 |
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
 选修4.1:几何证明选讲
选修4.1:几何证明选讲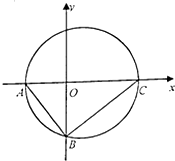 如图所示,在Rt△ABC中,已知A(-2,0),直角顶点B(0,-2
如图所示,在Rt△ABC中,已知A(-2,0),直角顶点B(0,-2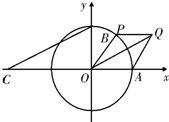 如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.
如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.