题目内容
已知a∈[-1，1]，不等式x2+（a-4）x+4-2a＞0恒成立，则x的取值范围为（ ）
| A、（-∞，2）∪（3，+∞） |
| B、（-∞，1）∪（2，+∞） |
| C、（-∞，1）∪（3，+∞） |
| D、（1，3） |
考点：函数恒成立问题
专题：不等式的解法及应用
分析：把不等式看作是关于a的一元一次不等式，然后构造函数f（a）=（x-2）a+x2-4x+4，由不等式在[-1，1]上恒成立，得到
，求解关于a的不等式组得x得取值范围．
|
解答：
解：令f（a）=（x-2）a+x2-4x+4，
则不等式x2+（a-4）x+4-2a＞0恒成立转化为f（a）＞0恒成立（a∈[-1，1]）．
∴有
，即
，
整理得：
，
解得：x＜1或x＞3．
∴x的取值范围为（-∞，1）∪（3，+∞）．
故选：C．
则不等式x2+（a-4）x+4-2a＞0恒成立转化为f（a）＞0恒成立（a∈[-1，1]）．
∴有
|
|
整理得：
|
解得：x＜1或x＞3．
∴x的取值范围为（-∞，1）∪（3，+∞）．
故选：C．
点评：本题考查了恒成立问题，体现了数学转化思想方法，“更换主元”是解答该题的关键，是中档题．
练习册系列答案
相关题目
圆x2+y2-6x=0与圆x2+y2+8y+12=0的位置关系是（ ）
| A、相离 | B、相交 | C、外切 | D、内切 |
一个物体的运动方程是s=2t2+at+1，该物体在t=1时的瞬时速度为3，则a=（ ）
| A、1 | B、0 | C、-1 | D、7 |
函数y=log
（-x2+2x+3）的单调递减区间为（ ）
| 1 |
| 2 |
| A、（0，+∞） |
| B、（-1，3） |
| C、（-1，1] |
| D、[1，3） |
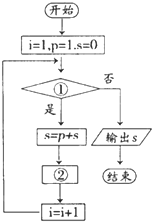给出15个数：1，2，4，7，11，…，要计算这15个数的和，现给出解决该问题的程序框图（如图所示），那么框图中判断框①处和执行框②处应分别填入（ ）| A、i≤16？； p=p+i-1 |
| B、i≤14？； p=p+i+1 |
| C、i≤15？； p=p+i+1 |
| D、i≤15？； p=p+i |
已知复数z满足z=
（i为虚数单位），则复数z所对应的点所在象限为（ ）
| 3+i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
i是虚数单位，复数z=i-1，则|z|=（ ）
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|