题目内容
已知回归方程
=1.5x-2，则原始数据（2，2）的残差
为（ ）
| ∧ |
| y |
| ∧ |
| e |
| A、-1 | B、1 | C、0 | D、0.5 |
考点：线性回归方程
专题：概率与统计
分析：将x=2代入回归方程计算出预报变量
的值，与2比较后可得答案．
| ∧ |
| y |
解答：
解：∵回归方程为
=1.5x-2，
当x=2时，
=1，
∵|1-2|=1，
故原始数据（2，2）的残差
为1，
故选：B．
| ∧ |
| y |
当x=2时，
| ∧ |
| y |
∵|1-2|=1，
故原始数据（2，2）的残差
| ∧ |
| e |
故选：B．
点评：本题考查的知识点是线性回归方程，残差的定义，难度不大，属于基础题．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
要得到函数y=
cosx的图象，需将函数y=
sin（2x+
）的图象上所有的点的变化正确的是（ ）
| 2 |
| 2 |
| π |
| 4 |
A、横坐标缩短到原来的
| ||||
B、横坐标缩短到原来的
| ||||
C、横坐标伸长到原来的2倍（纵坐标不变），再向左平行移动
| ||||
D、横坐标伸长到原来的2倍（纵坐标不变），再向右平行移动
|
已知x∈R，P=ex+e-x，Q=（sinx+cosx）2，下面的关系式一定成立的是（ ）
| A、?x0∈R，使P=Q |
| B、P＞Q |
| C、P≤Q |
| D、P＜Q |
已知平面上不共线的四点O，A，B，C，若
-4
+3
=0，则
=（ ）
| OA |
| OB |
| OC |
|
| ||
|
|
| A、3 | B、4 | C、5 | D、6 |
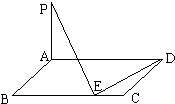如图：已知矩形ABCD中，AB=2，BC=a，若PA⊥面AC，在BC边上取点E，使PE⊥DE，则满足条件的E点有两个时，a的取值范围是（ ）| A、a＞4 | B、a≥4 |
| C、0＜a＜4 | D、0＜a≤4 |
在R上可导的函数f（x）的图形如图所示，则关于x的不等式x•f′（x）＜0的解集为（ ）
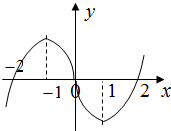
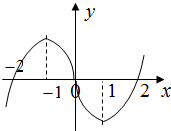
| A、（-∞，-1）∪（0，1） |
| B、（-1，0）∪（1，+∞） |
| C、（-2，-1）∪（1，2） |
| D、（-∞，-2）∪（2，+∞） |
（1
）0-（1-0.5-2）÷(
)
的值为（ ）
| 1 |
| 2 |
| 27 |
| 8 |
| 2 |
| 3 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
盒中有10支螺丝钉，其中3支是坏的，现在从盒中不放回地依次抽取两支，那么在第一支抽取为好的条件下，第二支是坏的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|