题目内容
两直线ρsin(θ+
)=11,ρsin(θ-
)=10的位置关系是( )
| π |
| 4 |
| π |
| 4 |
| A、垂直 | B、平行 |
| C、斜交 | D、以上都不正确 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把极坐标方程化为直角坐标方程,利用直线垂直与斜率的关系即可判断出.
解答:
解:两直线ρsin(θ+
)=11,ρsin(θ-
)=10
分别化为:ρ(
sinθ+
cosθ)=11,ρ(
sinθ-
cosθ)=10,
∴y+x=11
,y-x=10
.
两条直线的斜率分别为-1,1,
∴此两条直线垂直.
故选:A.
| π |
| 4 |
| π |
| 4 |
分别化为:ρ(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴y+x=11
| 2 |
| 2 |
两条直线的斜率分别为-1,1,
∴此两条直线垂直.
故选:A.
点评:本题考查了极坐标方程化为直角坐标方程、直线垂直与斜率的关系,属于基础题.

练习册系列答案
相关题目
若a∈{1,2,3,5},b∈{1,2,3,5},则方程y=
x表示的不同直线条数为( )
| b |
| a |
| A、11 | B、12 | C、13 | D、14 |
已知cos20°=k,则sin50°=( )
| A、2k2-1 |
| B、1-k2 |
| C、k2-1 |
| D、1-2k2 |
在区间[0,3]上任取一个实数,则此实数小于1的概率为( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知x∈R,P=ex+e-x,Q=(sinx+cosx)2,下面的关系式一定成立的是( )
| A、?x0∈R,使P=Q |
| B、P>Q |
| C、P≤Q |
| D、P<Q |
已知数列{an}为等比数列,a4+a7=2,a5•a6=-8,则a1+a10的值为( )
| A、7 | B、-5 | C、5 | D、-7 |
已知平面上不共线的四点O,A,B,C,若
-4
+3
=0,则
=( )
| OA |
| OB |
| OC |
|
| ||
|
|
| A、3 | B、4 | C、5 | D、6 |
在R上可导的函数f(x)的图形如图所示,则关于x的不等式x•f′(x)<0的解集为( )
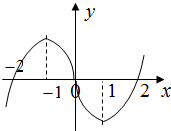
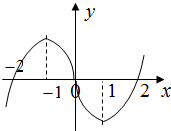
| A、(-∞,-1)∪(0,1) |
| B、(-1,0)∪(1,+∞) |
| C、(-2,-1)∪(1,2) |
| D、(-∞,-2)∪(2,+∞) |
已知锐角θ满足sin2θ=a,则sinθ+cosθ的值是( )
A、
| ||||
B、
| ||||
C、±
| ||||
D、
|