题目内容
用1,2,3,4,5排成一个五位数,则使任两个相邻数码之差至少是2的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:根据已知计算出用1,2,3,4,5排成一个五位数的方法总数,和任两个相邻数码之差至少是2的方法种数,代入古典概型概率计算公式,可得答案.
解答:
解:用1,2,3,4,5排成一个五位数共有
=120种不同的排列方法,
其中任两个相邻数码之差至少是2的排法有14种,分别为:
13524,14253,24135,24153,25314,31425,31524,
35142,35241,41352,42513,42531,52413,53142,
故使任两个相邻数码之差至少是2的概率P=
=
,
故选:A
| A | 5 5 |
其中任两个相邻数码之差至少是2的排法有14种,分别为:
13524,14253,24135,24153,25314,31425,31524,
35142,35241,41352,42513,42531,52413,53142,
故使任两个相邻数码之差至少是2的概率P=
| 14 |
| 120 |
| 7 |
| 60 |
故选:A
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
相关题目
已知cos20°=k,则sin50°=( )
| A、2k2-1 |
| B、1-k2 |
| C、k2-1 |
| D、1-2k2 |
已知平面上不共线的四点O,A,B,C,若
-4
+3
=0,则
=( )
| OA |
| OB |
| OC |
|
| ||
|
|
| A、3 | B、4 | C、5 | D、6 |
在R上可导的函数f(x)的图形如图所示,则关于x的不等式x•f′(x)<0的解集为( )
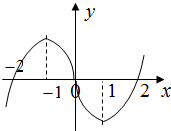
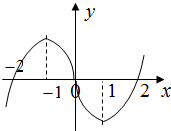
| A、(-∞,-1)∪(0,1) |
| B、(-1,0)∪(1,+∞) |
| C、(-2,-1)∪(1,2) |
| D、(-∞,-2)∪(2,+∞) |
(1
)0-(1-0.5-2)÷(
)
的值为( )
| 1 |
| 2 |
| 27 |
| 8 |
| 2 |
| 3 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
函数y=
sin(2x-
)的图象可以看作是函数y=
sin2x的图象( )
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
盒中有10支螺丝钉,其中3支是坏的,现在从盒中不放回地依次抽取两支,那么在第一支抽取为好的条件下,第二支是坏的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知锐角θ满足sin2θ=a,则sinθ+cosθ的值是( )
A、
| ||||
B、
| ||||
C、±
| ||||
D、
|