题目内容
已知平面向量的集合A到A的映射f:
→f(
)=
-2(
•
)
(
为常向量)满足f(
)•f(
)=
•
对任意
,
∈A恒成立,则
的坐标不可能是( )
| x |
| x |
| x |
| x |
| a |
| a |
| a |
| x |
| y |
| x |
| y |
| x |
| y |
| a |
| A、(0,0) | ||||||||
B、(
| ||||||||
C、(-
| ||||||||
D、(
|
考点:映射
专题:函数的性质及应用,平面向量及应用
分析:通过赋值列出关于向量的方程,通过向量的运算法则化简方程,得到
满足的条件.
| a |
解答:
解:令
=
,则f(
)•f(
)=
•
=[
-2(
•
)
]2=
2-4(
•
)2+4[(
•
)
]2,
即-4(
•
)2+4[(
•
)
]2=0,
∴(
•
)2(
2-1)=0
∴
=0或|
|=1,
故选:D.
| y |
. |
| x |
| x |
| x |
| x |
| x |
| x |
| x |
| a |
| a |
| x |
| x |
| a |
| x |
| a |
| a |
即-4(
| x |
| a |
| x |
| a |
| a |
∴(
| x |
| a |
| a |
∴
| a |
| a |
故选:D.
点评:本题以映射为载体考查向量的运算法则及向量的运算律,难度不大,属于基础题.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
若a∈{1,2,3,5},b∈{1,2,3,5},则方程y=
x表示的不同直线条数为( )
| b |
| a |
| A、11 | B、12 | C、13 | D、14 |
设f(x)为可导函数,且满足
=-1,则函数y=f(x)在x=1处的导数值为( )
| lim |
| △x→0 |
| f(1+△x)-f(1) |
| △x |
| A、1 | B、-1 |
| C、1或-1 | D、以上答案都不对 |
要得到函数y=
cosx的图象,需将函数y=
sin(2x+
)的图象上所有的点的变化正确的是( )
| 2 |
| 2 |
| π |
| 4 |
A、横坐标缩短到原来的
| ||||
B、横坐标缩短到原来的
| ||||
C、横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动
| ||||
D、横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动
|
若直线
(t为参数)与直线4x+ky=1垂直,则常数k=( )
|
| A、7 | B、5 | C、4 | D、6 |
已知cos20°=k,则sin50°=( )
| A、2k2-1 |
| B、1-k2 |
| C、k2-1 |
| D、1-2k2 |
在区间[0,3]上任取一个实数,则此实数小于1的概率为( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
在R上可导的函数f(x)的图形如图所示,则关于x的不等式x•f′(x)<0的解集为( )
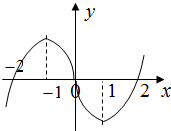
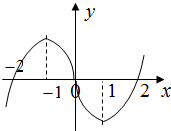
| A、(-∞,-1)∪(0,1) |
| B、(-1,0)∪(1,+∞) |
| C、(-2,-1)∪(1,2) |
| D、(-∞,-2)∪(2,+∞) |