题目内容
若对区间[a,b]上的任意x1,x2,当x1<x2时,f(x1)≤f(x2),我们称f(x)在[a,b]上为不减函数.已知f(x)是定义在[0,1]上的不减函数,且满足f(0)=0,f(1-x)=1-f(x),f(1-
x)=1-
f(x),则f(
)的值为( )
| 1 |
| 3 |
| 1 |
| 2 |
| 7 |
| 8 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
考点:抽象函数及其应用
专题:计算题,探究型
分析:根据条件f(1-x)=1-f(x),f(1-
x)=1-
f(x),可得:f(1-
x)=1-f(
x)=1-
f(x),
即f(
x)=
f(x),赋值求解即可.
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
即f(
| 1 |
| 3 |
| 1 |
| 2 |
解答:
解:对区间[a,b]上的任意x1,x2,当x1<x2时,f(x1)≤f(x2),我们称f(x)在[a,b]上为不减函数.
∵f(x)是定义在[0,1]上的不减函数,且满足f(0)=0,f(1-x)=1-f(x),
∴f(1-
x)=1-f(
x)=1-
f(x),
即f(
x)=
f(x),
所以f(1-x)+f(x)=1与f(
x)=
f(x)同时成立,且x在[0,1]上,
∵f(0)=0,∴f(1)=1,
∴赋值可得:f(
)=
,f(
)=
f(1)=
,f(
)=
,f(
)=
×f(
)=
,
计算可得f(
)=1-
=
故选:B
∵f(x)是定义在[0,1]上的不减函数,且满足f(0)=0,f(1-x)=1-f(x),
∴f(1-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
即f(
| 1 |
| 3 |
| 1 |
| 2 |
所以f(1-x)+f(x)=1与f(
| 1 |
| 3 |
| 1 |
| 2 |
∵f(0)=0,∴f(1)=1,
∴赋值可得:f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 3 |
| 8 |
| 1 |
| 4 |
计算可得f(
| 7 |
| 8 |
| 1 |
| 4 |
| 3 |
| 4 |
故选:B
点评:本题考查了抽象函数的应用,赋值计算给定的函数值,注意观察转化.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
在区间[0,3]上任取一个实数,则此实数小于1的概率为( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
在R上可导的函数f(x)的图形如图所示,则关于x的不等式x•f′(x)<0的解集为( )
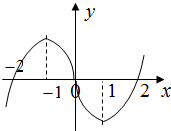
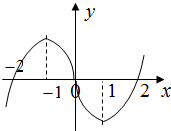
| A、(-∞,-1)∪(0,1) |
| B、(-1,0)∪(1,+∞) |
| C、(-2,-1)∪(1,2) |
| D、(-∞,-2)∪(2,+∞) |
函数y=
sin(2x-
)的图象可以看作是函数y=
sin2x的图象( )
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
盒中有10支螺丝钉,其中3支是坏的,现在从盒中不放回地依次抽取两支,那么在第一支抽取为好的条件下,第二支是坏的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=sin(-x+
)在x∈[0,2π]的一个单调递增区间是( )
| π |
| 4 |
A、[0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
已知锐角θ满足sin2θ=a,则sinθ+cosθ的值是( )
A、
| ||||
B、
| ||||
C、±
| ||||
D、
|
若f(x)是(-a,a)上的可导奇函数,且f'(x)不恒为零,则f'(x)在(-a,a)上( )
| A、必为奇函数 |
| B、必为偶函数 |
| C、是非奇非偶函数 |
| D、可能为奇函数,也可能是偶函数 |