题目内容
已知某几何体的三视图如图所示,则该几何体的体积是 .
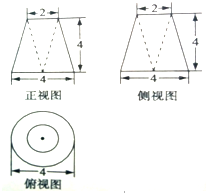

考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:几何体是圆台挖去等高的圆锥,根据三视图知圆锥的底面为圆台的上底面,判断圆台的高及上、下底面半径,把数据代入圆台与圆锥的体积公式计算.
解答:
解:由三视图知:几何体是圆台挖去等高的圆锥,且圆锥的底面为圆台的上底面,顶点是圆台下底面的圆心,
其中圆台的高为4,上、下底面直径为2和4,
∴几何体的体积V=
π×(12+22+1×2)×4-
π×12×4=8π.
故答案为:8π.
其中圆台的高为4,上、下底面直径为2和4,
∴几何体的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:8π.
点评:本题考查了由三视图求几何体的体积,根据三视图判断几何体的形状及数据所对应的几何量是解题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
若直线y=|
|x+1与直线y=|
|x平行,
,
为非零向量,则必有( )
| a |
| b |
| a |
| b |
A、
| ||||||||
B、
| ||||||||
C、(
| ||||||||
D、(
|
在△ABC中,∠BAC=60°,点O满足2
+
+
=
,且OC⊥OA,则
的值为( )
| OA |
| OB |
| OC |
| 0 |
| AB |
| AC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
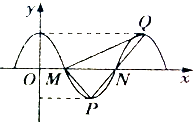 已知函数f(x)=Acosωx(ω>0)的部分图象如图所示,且∠MQP=
已知函数f(x)=Acosωx(ω>0)的部分图象如图所示,且∠MQP= 若如图框图所给程序运行的结果为S=360,那么判断框中应填入的关于k的判断条件是k<
若如图框图所给程序运行的结果为S=360,那么判断框中应填入的关于k的判断条件是k<