Question

已知函数f（x）=cos⁴x-2sinxcosx-sin⁴x（x∈R）
（1）求函数f（x）的最小正周期；
（2）在给出的直角坐标系中，画出函数y=f（x）在区间[-

π

2

，

π

2

]上的图象．

Answer 1

考点：三角函数中的恒等变换应用

专题：三角函数的图像与性质

分析：（I）利用二倍角公式，两角差的正弦公式，化简函数f（x）的解析式为一个角的一个函数名称的形式，然后利用T=

2π

|ω|

求周期．
（2）利用描点法画出图象．

解答： 解（1）已知函数f（x）=cos⁴x-2sinxcosx-sin⁴x=（cos²x+sin²x）（cos²x-sin²x）-sin2x
=cos2x-sin2x=-

2

sin（2x-

π

4

），∵T=

2π

2

=π，
∴函数f（x）的最小正周期为π；
（2）列表如下：

x	π 8	3π 8	5π 8	7π 8	9π 8
2x- π 4	0	π 2	π	3π 2	2π
2 sin（2x- π 4 ）	0	2	0	- 2	0

描点画图如下：

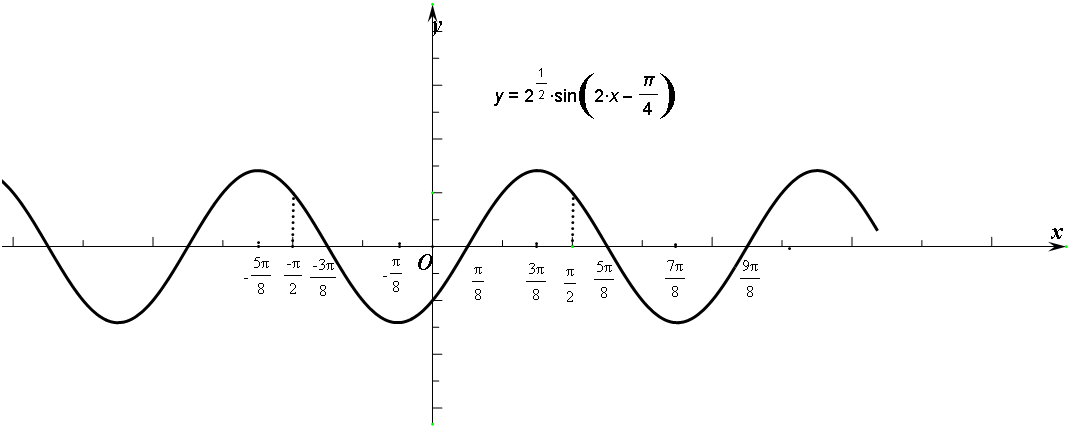
虚线之间的部分即为函数y=f（x）在区间[-

π

2

，

π

2

]上的图象．

点评：本题考查二倍角公式的应用，两角差的正弦公式，正弦函数的单调性，周期性，定义域和值域，化简函数f（x）的解析式是解题的关键．