题目内容
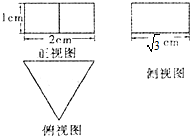 某个几何体的三视图如图所示,其中俯视图为等边三角形,则该几何体的表面积是( )
某个几何体的三视图如图所示,其中俯视图为等边三角形,则该几何体的表面积是( )A、
| ||
B、6+
| ||
C、6+2
| ||
D、6+3
|
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:由几何体的三视图知:该几何体是正三棱柱ABC-A1B1C1,底面△ABC的边长是2,高AA1=1,由此能求出该几何体的表面积.
解答:
解:由几何体的三视图知:
该几何体是正三棱柱ABC-A1B1C1,
底面△ABC的边长是2,高AA1=1,
∴该几何体的表面积:
S=2×(
×2×2×sin60°)+3×(2×1)
=6+2
.
故选:C.

该几何体是正三棱柱ABC-A1B1C1,
底面△ABC的边长是2,高AA1=1,
∴该几何体的表面积:
S=2×(
| 1 |
| 2 |
=6+2
| 3 |
故选:C.
点评:本题考查几何体的表面积的求法,是中档题,解题时要认真审题,注意三视图的合理运用.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
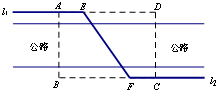 如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB=
如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB= 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.