题目内容
下列函数中,值域为(0,+∞)的是( )
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
考点:函数的值域
专题:函数的性质及应用
分析:A中的函数变成:y=|x-1|≥0,B中的函数可以变成:y=1+
,由x∈(0,+∞)可得到y∈(1,2),C中的函数的值域显然不连续,所以便选D.
| 1 |
| x+1 |
解答:
解:A.y=
=|x-1|≥0,∴该函数的值域为[0,+∞);
B.y=
=1+
,∵x>0,∴x+1>1,0<
<1,1<1+
<2,∴该函数的值域为(1,2);
C.∵x∈N,即该函数的定义域是由孤立的自然数组成,所以值域也应是不连续的数构成;
D.y=
>0,∴该函数的值域为(0,+∞),所以该选项正确.
故选D.
| x2-2x+1 |
B.y=
| x+2 |
| x+1 |
| 1 |
| x+1 |
| 1 |
| x+1 |
| 1 |
| x+1 |
C.∵x∈N,即该函数的定义域是由孤立的自然数组成,所以值域也应是不连续的数构成;
D.y=
| 1 |
| |x+1| |
故选D.
点评:考查值域的概念,以及通过化简原函数解析式来求函数值域的方法,由定义域的不连续便得到值域不连续.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a、b是不相等的正数,且a、x、y、b成等差数列,a、m、n、b成等比数列,则下列关系成立的是( )
| A、x+y>m+n |
| B、x+y=m+n |
| C、x+y<m+n |
| D、不能确定 |
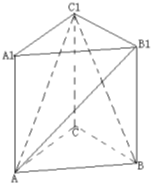 (文)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=2.
(文)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=2.