题目内容
9.若方程|lnx|=a有两个不等的实根x1和x2,则x1+x2的取值范围是( )| A. | (1,+∞) | B. | ($\sqrt{2}$,+∞) | C. | (2,+∞) | D. | (0,1) |
分析 利用y=|lnx|的单调性判断x1,x2的范围,根据对数的运算性质得出x1x2=1,再利用基本不等式即可得出答案.
解答 解:令f(x)=|lnx|=$\left\{\begin{array}{l}{lnx,x≥1}\\{-lnx,0<x<1}\end{array}\right.$,
∴f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,且f(1)=0,
∵方程|lnx|=a有两个不等的实根x1和x2,不妨设x1<x2,则0<x1<1<x2,
且-lnx1=lnx2=a,∴lnx1+lnx2=lnx1x2=0,∴x1x2=1,
∴x1+x2=x1+$\frac{1}{{x}_{1}}$>2,
故选C.
点评 本题考查了对数函数的图象与性质,对数的运算性质和基本不等式的应用,属于中档题.

练习册系列答案
相关题目
19.将函数$f(x)=2sin({x+\frac{π}{6}})+1$的图象向右平移$\frac{π}{3}$个单位,再把所有点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),得函数y=g(x)的图象,则g(x)图象的一个对称中心为( )
| A. | $({\frac{π}{6},0})$ | B. | $({\frac{π}{12},0})$ | C. | $({\frac{π}{6},1})$ | D. | $({\frac{π}{12},1})$ |
20.设z是复数,|z-i|≤2(i是虚数单位),则|z|的最大值是 ( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
19.集合A={x|y=lg(x-2)},B={y|y=2x,x≥0},则(∁RA)∩B=( )
| A. | (0,2) | B. | [0,2] | C. | [1,2] | D. | (1,2) |
 在△ABC中,角A、B、C对边分别为a、b、c,a2+b2+c2=ab+bc+ca.
在△ABC中,角A、B、C对边分别为a、b、c,a2+b2+c2=ab+bc+ca.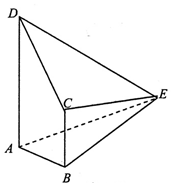 如图,在四棱锥E-ABCD中,平面CDE⊥平面ABCD,∠DAB=∠ABC=90°,AB=BC=1,AD=ED=3,EC=2.
如图,在四棱锥E-ABCD中,平面CDE⊥平面ABCD,∠DAB=∠ABC=90°,AB=BC=1,AD=ED=3,EC=2.