题目内容
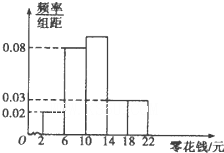为了引导学生树立正确的消费观，某校调查了全校1000名学生每天零花钱的数量，绘制频率分布直方图如图，则每天的零花钱数量在[6，14）内的学生人数为考点：频率分布直方图
专题：概率与统计
分析：根据频率分布直方图，求出每天的零花钱数量在[6，14）内的频率，即可求得对应的学生数．
解答：
解：根据频率分布直方图，得
每天的零花钱数量在[6，14）内的频率为
1-（0.02+0.03+0.03）×4=0.68，
∴每天的零花钱数量在[6，14）内的学生数为
1000×0.68=680；
故答案为：680．
每天的零花钱数量在[6，14）内的频率为
1-（0.02+0.03+0.03）×4=0.68，
∴每天的零花钱数量在[6，14）内的学生数为
1000×0.68=680；
故答案为：680．
点评：本题考查了利用频率分布直方图，求某一范围内的频率和频数的问题，解题时应明确频数、频率以及各小长方形面积的关系，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知a＞0，函数f（x）=
x3-ax2+x+1．
（Ⅰ）若f（x）在x=x1，x=x2处取得极值，且1＜
≤5，求实数a的取值范围；
（Ⅱ）当x≥2时，求3f（x）+|f′（a）-1|的最小值．
| a |
| 3 |
（Ⅰ）若f（x）在x=x1，x=x2处取得极值，且1＜
| x2 |
| x1 |
（Ⅱ）当x≥2时，求3f（x）+|f′（a）-1|的最小值．
已知数列{an}中，a1=25，4an+1=4an-7（n∈N*），若其前n项和为Sn，则Sn的最大值为（ ）
| A、15 | ||
| B、750 | ||
C、
| ||
D、
|