题目内容
在平面直角坐标系xOy中,点P到两圆C1:x2+y2-2
y+2=0与C2:x2+y2+2
y-3=0的圆心的距离之和等于4,设点P的轨迹为C.
(1)求C的方程;
(2)设直线y=kx+1与C交于A,B两点.问k为何值时
⊥
?
| 3 |
| 3 |
(1)求C的方程;
(2)设直线y=kx+1与C交于A,B两点.问k为何值时
| OA |
| OB |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)根据椭圆的定义即可求出对应的方程.
(2)利用直线和椭圆的位置关系,将条件转换为一元二次函数即可得到结论.
(2)利用直线和椭圆的位置关系,将条件转换为一元二次函数即可得到结论.
解答:
解:(1)由已知得两圆的圆心坐标分别为C1:(0,
),C2:(0,-
),
设P(x,y),由椭圆定义可知,点P的轨迹C是以C1(0,
),C2(0,-
)为焦点,长半轴长为2的椭圆.
它的短半轴长b=
=1,
故曲线C的方程为x2+
=1.
(2)设A(x1,y1),B(x2,y2),将直线y=kx+1代入x2+
=1,
消去y并整理得(k2+4)x2+2kx-3=0,
∵k2+4≠0,△=4k2+12(k2+4)=16(k2+3)>0,
∴x1+x2=-
,x1x2=-
.
又y1y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1,
若
⊥
,
则x1x2+y1y2=0,
即x1x2+y1y2=x1x2+k2x1x2+k(x1+x2)+1=
=0
即-4k2+1=0,
解得k=±
.
| 3 |
| 3 |
设P(x,y),由椭圆定义可知,点P的轨迹C是以C1(0,
| 3 |
| 3 |
它的短半轴长b=
22-(
|
故曲线C的方程为x2+
| y2 |
| 4 |
(2)设A(x1,y1),B(x2,y2),将直线y=kx+1代入x2+
| y2 |
| 4 |
消去y并整理得(k2+4)x2+2kx-3=0,
∵k2+4≠0,△=4k2+12(k2+4)=16(k2+3)>0,
∴x1+x2=-
| 2k |
| k2+4 |
| 3 |
| k2+4 |
又y1y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1,
若
| OA |
| OB |
则x1x2+y1y2=0,
即x1x2+y1y2=x1x2+k2x1x2+k(x1+x2)+1=
| -4k2+1 |
| k2+4 |
即-4k2+1=0,
解得k=±
| 1 |
| 2 |
点评:本题考查椭圆的定义和方程的求法,以及直线和椭圆的位置关系的应用,综合性较强,运算量较大.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
已知数列{an}中,a1=25,4an+1=4an-7(n∈N*),若其前n项和为Sn,则Sn的最大值为( )
| A、15 | ||
| B、750 | ||
C、
| ||
D、
|
某学习小组男女生共8人,现从男生中选2人,女生中选1人,分别去做3中不同的工作,共有90种不同的选法,则男女生人数为( )
| A、2,6 | B、3,5 |
| C、5,3 | D、6,2 |
 某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如图所示.根据学生体质健康标准,成绩不低于76的为优良.
某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如图所示.根据学生体质健康标准,成绩不低于76的为优良.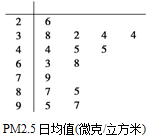 通常把大气中直径小于或等于2.5微米的颗粒物(也称为可入肺颗粒物)称为PM2.5.我国PM2.5标准采用世卫组织设定的最宽限值,空气质量与PM2.5的关系如下表:
通常把大气中直径小于或等于2.5微米的颗粒物(也称为可入肺颗粒物)称为PM2.5.我国PM2.5标准采用世卫组织设定的最宽限值,空气质量与PM2.5的关系如下表: