题目内容
已知定义在R上的函数f(x)满足:f(x)=
,且f(x+2)=f(x),g(x)=
,则方程f(x)=g(x)在区间[-5,1]上的所有实根之和为( )
|
| 2x+5 |
| x+2 |
| A、-5 | B、-6 | C、-7 | D、-8 |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:将方程根的问题转化为函数图象的交点问题,由图象读出即可.
解答:
解:∵f(x)=
,且f(x+2)=f(x),
∴f(x-2)-2=
;
又g(x)=
,
∴g(x)=2+
,
∴g(x-2)-2=
,
当x≠2k-1,k∈Z时,
上述两个函数都是关于(-2,2)对称,;
由图象可得:方程f(x)=g(x)在区间[-5,1]上的实根有3个,
x1=-3,x2满足-5<x2<-4,x3满足0<x3<1,x2+x3=-4;
∴方程f(x)=g(x)在区间[-5,1]上的所有实根之和为-7.
故答案为;C.
|
∴f(x-2)-2=
|
又g(x)=
| 2x+5 |
| x+2 |
∴g(x)=2+
| 1 |
| x+2 |
∴g(x-2)-2=
| 1 |
| x |
当x≠2k-1,k∈Z时,
上述两个函数都是关于(-2,2)对称,;
由图象可得:方程f(x)=g(x)在区间[-5,1]上的实根有3个,
x1=-3,x2满足-5<x2<-4,x3满足0<x3<1,x2+x3=-4;
∴方程f(x)=g(x)在区间[-5,1]上的所有实根之和为-7.
故答案为;C.

点评:本题考查函数的零点与方程根的关系以及数形结合的思想,数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质.

练习册系列答案
相关题目
若直线y=2x+b被圆(x+1)2+y2=4所截得的弦最长,则b等于( )
| A、-1 | B、0 | C、1 | D、2 |
已知数列{an}中,a1=25,4an+1=4an-7(n∈N*),若其前n项和为Sn,则Sn的最大值为( )
| A、15 | ||
| B、750 | ||
C、
| ||
D、
|
如图是一个组合几何体的三视图,则该几何体的体积是( )


A、
| ||||
B、
| ||||
| C、12+64π | ||||
| D、36+128π |
 某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如图所示.根据学生体质健康标准,成绩不低于76的为优良.
某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如图所示.根据学生体质健康标准,成绩不低于76的为优良.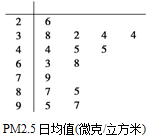 通常把大气中直径小于或等于2.5微米的颗粒物(也称为可入肺颗粒物)称为PM2.5.我国PM2.5标准采用世卫组织设定的最宽限值,空气质量与PM2.5的关系如下表:
通常把大气中直径小于或等于2.5微米的颗粒物(也称为可入肺颗粒物)称为PM2.5.我国PM2.5标准采用世卫组织设定的最宽限值,空气质量与PM2.5的关系如下表: