题目内容
C.(不等式选做题)若关于x 的方程x2+x+|a-
|=0(a∈R)有实根,则a的取值范围是 .
| 1 |
| 4 |
考点:绝对值不等式
专题:计算题,不等式的解法及应用
分析:根据题意,利用一元二次方程根的判别式可得△=12-4•|a-
|≥0,化简得|a-
|≤
,解之即可得到实数a的取值范围.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:∵关于x的方程x2+x+|a-
|=0(a∈R)有实根,
∴△=12-4•|a-
|≥0,即|a-
|≤
,
可得-
≤a-
≤
,解得0≤a≤
,
∴实数a的取值范围是[0,
].
故答案为:[0,
]
| 1 |
| 4 |
∴△=12-4•|a-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
可得-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
∴实数a的取值范围是[0,
| 1 |
| 2 |
故答案为:[0,
| 1 |
| 2 |
点评:本题已知关于x的一元二次方程有实数根,求参数a的取值范围.着重考查了一元二次方程根的判别式和绝对值不等式的解法等知识,属于基础题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
一个空间几何体的三视图及其相关数据如图所示,则这个空间几何体的表面积是( )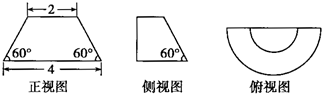

A、
| ||||
B、
| ||||
| C、11π | ||||
D、
|
若tanθ=2,则2sin2θ-sinθcosθ-cos2θ=( )
| A、5 | ||
| B、1 | ||
C、
| ||
D、
|
已知函数f(x)=|x2-6|,若a<b<0,且f(a)=f(b),则a2b的最小值是( )
| A、-16 | B、-12 |
| C、-10 | D、-8 |
若直线l:4x+3y+a=0和圆C:x2+y2+2x-4y+1=0有公共点,则实数a的取值范围是( )
| A、[-12,8] |
| B、[-8,12] |
| C、[-22,18] |
| D、[-18,22] |
已知关于x的不等式组
的整数解只有6个,则a的取值范围是( )
|
| A、(-∞,-4) | ||
| B、[-5,-4) | ||
| C、(-5,+∞) | ||
D、(-5,-
|