题目内容
13.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点为F1,F2,若点P在椭圆上,且满足|PO|2=|PF1|•|PF2|(其中O为坐标原点),则称点P为“*”点,则椭圆上的“*”点有4个.分析 设出椭圆上的点P(x0,y0),利用焦半径公式,表示出|PO|2=|PF1|•|PF2|,求出点的坐标,得出结论.
解答 解:设椭圆上的点P(x0,y0),则$\frac{{x}_{0}^{2}}{{a}^{2}}+\frac{{y}_{0}^{2}}{{b}^{2}}=1$,y02=b2(1-$\frac{{x}_{0}^{2}}{{a}^{2}}$),
椭圆的第二定义可知:|PF1|=a-ex0,|PF2|=a+ex0,
因为|PO|2=|PF1|•|PF2|,则x02+y02=a2-e2x02,
则有x02+b2(1-$\frac{{x}_{0}^{2}}{{a}^{2}}$)=x02+y02,解得x0=±$\frac{\sqrt{2}a}{2}$,
因此满足条件的有四个点,
故答案为:4.
点评 本题考查了椭圆的新定义问题,解题时应利用焦半径列出方程,求出点的坐标,是基础题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
3.已知集合A={x|x2-x-2<0},$B=\left\{{x|{{log}_4}x<\frac{1}{2}}\right\}$,则( )
| A. | A∩B=∅ | B. | ∁UA∪B=R | C. | A∩B=B | D. | A∪B=B |
4.执行如图2所示的程序框图,若输出S=7,则输入k(k∈N*)的值为( )

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
18.某人向平面区域$|x|+|y|≤\sqrt{2}$内任意投掷一枚飞镖,则飞镖恰好落在单位圆x2+y2=1内的概率为( )
| A. | $\frac{π}{4}$ | B. | $\frac{{\sqrt{3}π}}{4}$ | C. | $\frac{π}{8}$ | D. | $\frac{{\sqrt{3}π}}{6}$ |
2.下列函数为奇函数的是( )
| A. | y=$\sqrt{x}$ | B. | y=|sinx| | C. | y=ex-e-x | D. | y=cosx |
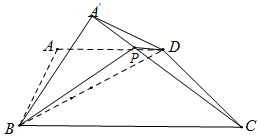 如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABC沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.
如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABC沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.