题目内容
3.用a、b表示两条不同的直线,α、β表示两个不同的平面,给出下列命题:①若a∥b,a∥α,则b∥α; ②若a⊥α,b⊥α,则a∥b;③若a∥α,b⊥α,则a⊥b; ④若a⊥α,α∥β,则a⊥β.
其中正确的是②③④.
分析 根据线面平行的判断定理知①错误;
由线面垂直的性质定理知②正确;
根据线面平行与垂直的定义知③正确;
根据线面垂直的定义与性质知④正确.
解答 解:对于①,a∥b,a∥α,
根据线面平行的判断定理知b∥α不一定成立,①错误;
对于②,a⊥α,b⊥α,
由线面垂直的性质定理知a∥b成立,②正确;
对于③,a∥α,b⊥α,
根据线面平行与垂直的定义知,a⊥b成立,③正确;
对于④,a⊥α,α∥β,
根据线面垂直的定义与性质值,a⊥β成立,④正确.
综上,正确的命题序号是②③④.
故答案为:②③④.
点评 本题考查了线面平行的判断与性质的应用问题,是综合题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
11.若双曲线$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{m}$=1的离心率为$\sqrt{m}$,则此双曲线的渐近线方程为( )
| A. | y=±$\frac{\sqrt{2}}{2}$x | B. | y=±$\frac{\sqrt{3}}{3}$x | C. | y=±$\frac{1}{2}$x | D. | y=±$\frac{1}{3}$x |
18.设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x)=f(x+4),且当x∈[-2,0]时,$f(x)={(\frac{1}{2})^x}-1$,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围为( )
| A. | (1,2) | B. | (2,+∞) | C. | (1,$\root{3}{4}$) | D. | ($\root{3}{4}$,2) |
8.若直线y=4x是曲线f(x)=x4+a的一条切线,则a的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.已知函数f(x)=$\frac{1}{2}$mcos2x+(m-2)sinx,其中1≤m≤2,若函数f(x)的最大值记为g(m),则g(m)的最小值为( )
| A. | -$\frac{1}{4}$ | B. | 1 | C. | 3-$\sqrt{3}$ | D. | $\sqrt{3}$-1 |
12.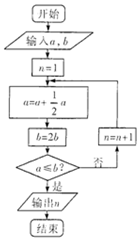 数学名著《算学启蒙》中有如下问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.”如图是源于其思想的一个程序框图,若输入的a,b的值分别为16,4,则输出的n的值为( )
数学名著《算学启蒙》中有如下问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.”如图是源于其思想的一个程序框图,若输入的a,b的值分别为16,4,则输出的n的值为( )
 数学名著《算学启蒙》中有如下问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.”如图是源于其思想的一个程序框图,若输入的a,b的值分别为16,4,则输出的n的值为( )
数学名著《算学启蒙》中有如下问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.”如图是源于其思想的一个程序框图,若输入的a,b的值分别为16,4,则输出的n的值为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
13.设x,y满足约束条件$\left\{\begin{array}{l}{2x+y-5≤0}\\{x-y-1≤0}\\{x≥1}\end{array}\right.$,若z=ax+y仅在点(2,1)处取得最大值,则a的取值范围是( )
| A. | (-∞,-1) | B. | (2,+∞) | C. | (0,2) | D. | (-1,+∞) |