题目内容
16．若变量x，y满足$\left\{\begin{array}{l}x-y+1≤0\\ x+y-5≤0\\ x≥0\end{array}\right.$，则点P（x，y）表示的区域的面积为4．分析 画出约束条件的可行域，求出点的坐标，然后求解区域的面积即可．
解答 
解：变量x，y满足$\left\{\begin{array}{l}x-y+1≤0\\ x+y-5≤0\\ x≥0\end{array}\right.$表示的可行域如图：
则点P（x，y）表示的区域的面积为：$\frac{1}{2}×4×2=4$．
故答案为：4．
点评 本题考查线性规划的简单应用，考查计算能力．
练习册系列答案
相关题目
5．泰华中学采取分层抽样的方法从高二学生中按照性别抽出20名学生作为样本，其选报文科与理科的情况如下表所示：
（Ⅰ）若在该样本中从报考文科的学生中随机地选出3人召开座谈会，试求3人中既有男生也有女生的概率；
（Ⅱ）能否在犯错误的概率不超过0.05的前提下认为泰华中学的高二学生选报文理科与性别有关？
注：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| 男 | 女 | |
| 文科 | 2 | 5 |
| 理科 | 10 | 3 |
（Ⅱ）能否在犯错误的概率不超过0.05的前提下认为泰华中学的高二学生选报文理科与性别有关？
注：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥k） | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
4．若sin（$\frac{π}{4}$-α）=$\frac{3}{5}$，-$\frac{π}{4}$＜α＜0，则cos2α=（ ）
| A． | -$\frac{24}{25}$ | B． | $\frac{1}{5}$ | C． | -$\frac{1}{5}$ | D． | $\frac{24}{25}$ |
11．“三元一次方程组的系数矩阵恰为单位矩阵”是“该方程组有唯一解”的（ ）条件．
| A． | 充分非必要 | B． | 必要非充分 | ||
| C． | 充要 | D． | 既非充分也非必要 |
1．函数$y=sin（2x+\frac{π}{3}）$图象中的一条对称轴的方程是（ ）
| A． | $x=\frac{π}{12}$ | B． | $x=\frac{π}{6}$ | C． | $x=\frac{π}{3}$ | D． | $x=-\frac{π}{12}$ |
8．函数f（x）=3x+$\frac{12}{x^2}$（x＞0）取得最小值时x为（ ）
| A． | 8 | B． | 9 | C． | 2 | D． | 6$\sqrt{6}$ |
5．函数f（x）=x3-3ax2+（2a+1）x既有极小值又有极大值，则a的取值范围为（ ）
| A． | -$\frac{1}{3}$＜a＜1 | B． | a＞1或a$＜-\frac{1}{3}$ | C． | -1$＜a＜\frac{1}{3}$ | D． | a$＞\frac{1}{3}$或a＜-1 |
6．如图，小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为（ ）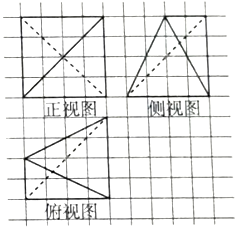
| A． | 8$\sqrt{3}$ | B． | $\frac{80}{3}$ | C． | 16$\sqrt{3}$ | D． | 32 |