Question

构造如图所示的数表，规则如下：先排两个l作为第一层，然后在每一层的相邻两个数之间插入这两个数和的a倍得下一层，其中a∈（0，

1

3

），设第n层中有a_n个数，这a_n个数的和为S_n（n∈N^*）．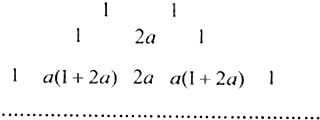
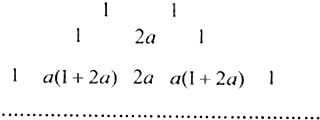
（I）求a_n；
（Ⅱ）证明：

n

2

≤

a1-1

S1

+

a2-1

S2

+…+

an-1

Sn

＜(

2

a+1

)n-1．

Answer 1

考点：数列与不等式的综合

专题：综合题,等差数列与等比数列

分析：（I）确定a_n+1-1=2（a_n-1），再求a_n；
（Ⅱ）先求S_n，再令bn=

an-1

Sn

，证b_n为单调增数列，从而证明

a1-1

S1

+

a2-1

S2

+…+

an-1

Sn

≥n(

a1-1

S1

)=

n

2

，对于正数x，y，由二项式定理

xn+yn

2

=

( x+y 2 + x-y 2 )n+( x+y 2 - x-y 2 )n

2

≥(

x+y

2

)n，即可证明右边成立．

解答： 解：（Ⅰ）由题意可得a₁=2，a_n+1=a_n+（a_n-1）=2a_n-1，∴a_n+1-1=2（a_n-1），
则an-1=(a1-1)•2n-1，得an=2n-1+1…（4分）
（Ⅱ）先求S_n，同（Ⅰ），S₁=2，S_n+1=S_n+2aS_n-2a=（2a+1）S_n-2a⇒Sn+1-1=(2a+1)(Sn-1)⇒Sn-1=(2a+1)n-1⇒Sn=(2a+1)n-1+1
令bn=

an-1

Sn

，则b_n=

2n-1

(2a+1)n-1+1

，
下证b_n为单调增数列：只需证b_n＜b_n+1?

2n-1

(2a+1)n-1+1

＜

2n

(2a+1)n+1

?2（2a+1）^n-1+2＞（2a+1）ⁿ+1?2(2a+1)n-1＞(2a+1)n?2＞2a+1?a＜

1

2

所以

a1-1

S1

+

a2-1

S2

+…+

an-1

Sn

≥n(

a1-1

S1

)=

n

2

又对于正数x，y，由二项式定理

xn+yn

2

=

( x+y 2 + x-y 2 )n+( x+y 2 - x-y 2 )n

2

≥(

x+y

2

)n
所以bn=

2n-1

(2a+1)n-1+1

=

1

( 2a+1 2 )n-1+( 1 2 )n-1

≤

1

2

(

2

2a+1 2 + 1 2

)n-1=

1

2

(

2

a+1

)n-1

a1-1

S1

+

a2-1

S2

+…+

an-1

Sn

≤

1

2

×

1-( 2 a+1 )n

1- 2 a+1

=

1

2

•

1+a

1-a

[(

2

a+1

)n-1]
又因为a＜

1

3

，所以

1+a

1-a

＜2，所以

a1-1

S1

+

a2-1

S2

+…+

an-1

Sn

＜(

2

a+1

)n-1…（12分）

点评：本题考查利用数表研究数列的通项，考查数列与不等式的联系，考查学生分析解决问题的能力，难度大．