题目内容

若3x2-xy+3y2=20，则8x2+23y2的最大值是
 
．
考点：函数的最值及其几何意义
专题：函数的性质及应用
分析：根据条件，利用三角换元法结合辅助角公式进行化简求解即可．
解答： 解：引入参数t，
∵3x2-xy+3y2=20，
∴（x-
y
6
）2+
35
36
y2=
20
3
，
设
x-
y
6
=
20
3
cosα
35
6
y=
20
3
sinα
，则
x=
20
3
cosα+
2
21
sinα
y=
12
21
sinα
，
代入8x2+23y2并化简得8x2+23y2=
2232
21
+
1128
21
sin(2α+θ)≤
2232
21
+
1128
21
=160，
当且仅当y=4x时，8x2+23y2的取得最大值为160，
故答案为：160
点评：本题主要考查考查利用三角换元法求式子的最值，是一道难度较大的竞赛试题．
练习册系列答案
相关题目
构造如图所示的数表，规则如下：先排两个l作为第一层，然后在每一层的相邻两个数之间插入这两个数和的a倍得下一层，其中a∈（0，
1
3
），设第n层中有an个数，这an个数的和为Sn（n∈N*）．
（I）求an；
（Ⅱ）证明：
n
2
≤
a1-1
S1
+
a2-1
S2
+…+
an-1
Sn
＜(
2
a+1
)n-1．
已知F1、F2分别是双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左右焦点，其右支上一点P，满足|PF1|=3，实轴长为1，M是y轴上一点，则
PM
•(
PF1
-
PF2
)=（　　）
A、
1
2
B、
3
2
C、
5
2
D、
7
2
已知曲线C1，C2的极坐标方程分别为ρ=4cos（θ+
π
6
）和ρcos（θ+
π
6
）=5．
（1）将C1，C2的方程化为直角坐标方程；
（2）设点P在曲线C1上，点Q在C2上，求|PQ|的最小值．
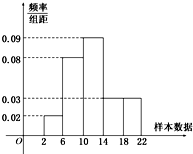如图是学校从走读生中随机调查200名走读生早上上学所需时间（单位：分钟）样本的频率分布直方图．
（1）学校所有走读生早上上学所需要的平均时间约是多少分钟？
（2）根据调查，距离学校500米以内的走读生上学时间不超过10分钟，距离学校1000米以内的走读生上学时间不超过20分钟．那么，距离学校500米以内的走读生和距离学校1000米以上的走读生所占全校走读生的百分率各是多少？
在平面直角坐标系xOy中，直线l与抛物线y2=2x相交于A，B两点．
（1）求证：“如果直线l过点（3，0），那么
OA
•
OB
=3”是真命题．
（2）写出（1）中命题的逆命题（直线l与抛物线y2=2x相交于A，B两点为大前提），判断它是真命题还是假命题，如果是真命题，写出证明过程；如果是假命题，则只需要举出一个反例说明即可．
计算：lg2+lne-lg102+49log73．
已知函数f（x）=sin（x-
π
6
）+
1
2
．
（1）若x∈[0，
π
2
]，f（x）=
11
10
，求cosx的值；
（2）在△ABC中，角A、B、C的对边分别是a、b、c，且满足2bcosA≤2c-
3
a，求f（B）的取值范围．
设函数f（x）=ex（ax2-x-1）（a∈R）．
（Ⅰ）若函数f（x）在R上单调递减，求a的取值范围
（Ⅱ）当a＞0时，求f（|sinx|）的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网