题目内容
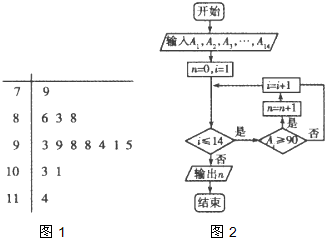
已知如图1所示是某学生的14次数学考试成绩的茎叶图，第1次到第14次的考试成绩依次记为A1，A2，…A14，图2是统计茎叶图中成绩在一定范围内考试次数的一个程序框图，则输出的n的值是（ ）
| A、8 | B、9 | C、10 | D、11 |
考点：程序框图,茎叶图
专题：算法和程序框图
分析：算法的功能是计算学生在14次数学考试成绩中，成绩大于等于90的次数，根据茎叶图可得成绩大于等于90的次数，即n值．
解答：
解：由程序框图知：算法的功能是计算学生在14次数学考试成绩中，成绩大于等于90的次数，
由茎叶图得，在14次测试中，成绩大于等于90的有：93、99、98、98、94、91、95、103、101、114共10次，
∴输出n的值为10．
故选：C．
由茎叶图得，在14次测试中，成绩大于等于90的有：93、99、98、98、94、91、95、103、101、114共10次，
∴输出n的值为10．
故选：C．
点评：本题借助茎叶图考查了循环结构的程序框图，根据框图的流程判断算法的功能是关键．
练习册系列答案
优学名师名题系列答案
相关题目
已知点A（-3，1，-4），B（3，-5，10）则线段AB的中点M的坐标为（ ）
| A、（0，-4，6） |
| B、（0，-2，3） |
| C、（0，2，3） |
| D、（0，-2，6） |
如果-1，m、n、p、-16成等比数列，那么（ ）
| A、n=-4，mp=-16 |
| B、n=-4，mp=16 |
| C、n=4，mp=16 |
| D、n=4，mp=-16 |
设一个正整数n可以表示为n=a02k+a12k-1+…+ak20（k∈N），其中a0=1，ai=0或1（1≤i≤k且i∈N），ai中为1的总个数记为f（n），例如f（1）=1，f（2）=1，f（3）=2，f（4）=1，则2f（1）+2f（2）+2f（3）+…+2f（31）=（ ）
| A、121 | B、243 |
| C、728 | D、729 |
执行如图所示的程序框图，当输入的x=9时，则输出的k=（ ）
| A、2 | B、3 | C、4 | D、5 |
已知圆的方程是（x-2）2+（y-3）2=4，则点P（-3，-2）满足（ ）
| A、是圆心 | B、在圆上 |
| C、在圆内 | D、在圆外 |
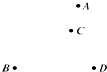如图A、B、C、D是某油田的四口油井，计划建三条路，将这四口油井连结起来（每条路只连结两口油井），那么不同的建路方案有（ ）| A、12种 | B、14种 |
| C、16种 | D、18种 |