题目内容
设一个正整数n可以表示为n=a02k+a12k-1+…+ak20(k∈N),其中a0=1,ai=0或1(1≤i≤k且i∈N),ai中为1的总个数记为f(n),例如f(1)=1,f(2)=1,f(3)=2,f(4)=1,则2f(1)+2f(2)+2f(3)+…+2f(31)=( )
| A、121 | B、243 |
| C、728 | D、729 |
考点:二项式系数的性质
专题:综合题,二项式定理
分析:31=1×24+1×23+1×22+1×21+1×20,则f(31)=5,与二项式定理结合,可转化为等比数列的前5项和,计算可得答案.
解答:
 解:根据题意,31=1×24+1×23+1×22+1×21+1×20,则f(31)=5.
解:根据题意,31=1×24+1×23+1×22+1×21+1×20,则f(31)=5.
列表如右:
由表格可得到如下规律:正整数k从2n到2n+1-1,
则∑2f(k)=3n-1.
∴2f(1)+2f(2)+2f(3)+…+2f(31)=30+31+32+33+34=121,
故选:A
 解:根据题意,31=1×24+1×23+1×22+1×21+1×20,则f(31)=5.
解:根据题意,31=1×24+1×23+1×22+1×21+1×20,则f(31)=5.列表如右:
由表格可得到如下规律:正整数k从2n到2n+1-1,
则∑2f(k)=3n-1.
∴2f(1)+2f(2)+2f(3)+…+2f(31)=30+31+32+33+34=121,
故选:A
点评:本题主要考查二项式系数的性质,解题的关键在于分析题意,透彻理解f(n)的含义,注意转化思想,结合二项式定理与等比数列的前n项和公式进行计算.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
已知函数f(x)=
(a为非零常数),则f(x)的图象满足( )
| (x-1)2+a |
| x-1 |
| A、关于点(1,0)对称 |
| B、关于点(1,1)对称 |
| C、关于原点对称 |
| D、关于直线x=1轴对称 |
已知如图1所示是某学生的14次数学考试成绩的茎叶图,第1次到第14次的考试成绩依次记为A1,A2,…A14,图2是统计茎叶图中成绩在一定范围内考试次数的一个程序框图,则输出的n的值是( )
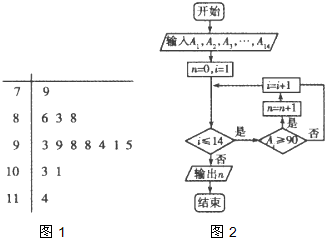

| A、8 | B、9 | C、10 | D、11 |
已知α是第三象限角,且sin(π-α)=-
,则tanα的值为( )
| 3 |
| 5 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知函数f(x)=x+cosx,则f′(
)=( )
| π |
| 6 |
A、
| ||||
B、
| ||||
C、1-
| ||||
D、
|
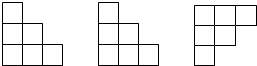 已知若干个正方体小木块堆放在一起形成的组合体的三视图如图所示,则所需小木块最少有多少个( )
已知若干个正方体小木块堆放在一起形成的组合体的三视图如图所示,则所需小木块最少有多少个( )| A、7个 | B、8个 | C、9个 | D、10个 |
已知函数f(x)=
,则f(2)=( )
|
| A、3 | B、2 | C、1 | D、0 |