题目内容

执行如图所示的程序框图，当输入的x=9时，则输出的k=（　　）
A、2B、3C、4D、5
考点：程序框图
专题：算法和程序框图
分析：根据框图的流程依次计算程序运行的结果，直到满足条件x＞2014，确定输出k的值．
解答： 解：由程序框图知：当输入x=9时，第一次循环x=10×9+9=99，k=1；
第二次循环x=10×99+9=999，k=2；
第三次循环x=10×999+9=9999，k=3．
满足条件x＞2014，跳出循环体，输出k=3．
故选：B．
点评：本题考查了循环结构的程序框图，根据框图的流程依次计算程序运行的结果是解答此类问题的抽样方法．
练习册系列答案
相关题目
已知A（2，3），B（3，0），且
AC
=-2
CB
，则点C的坐标为
 
．
设Z1，Z2是复数，下列命题：
①若|Z1-Z2|=0，则
.
Z1
=
.
Z2

②若Z1=
.
Z2
，则
.
Z1
=Z2
③若|Z1|=|Z2|，则Z1
.
Z1
=Z2
.
Z2

④若|Z1|=|Z2|，则Z12=Z22
以上真命题序号
 
．
已知如图1所示是某学生的14次数学考试成绩的茎叶图，第1次到第14次的考试成绩依次记为A1，A2，…A14，图2是统计茎叶图中成绩在一定范围内考试次数的一个程序框图，则输出的n的值是（　　）
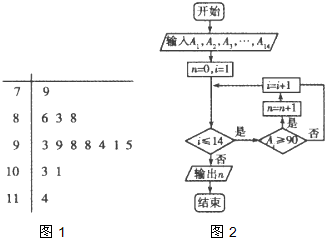
A、8B、9C、10D、11
已知cosα=-
3
3
，且tanα＜0，则sin2α的值等于（　　）
A、
2
2
3
B、
1
3
C、-
2
2
3
D、-
1
3
已知函数f（x）=x+cosx，则f′（
π
6
）=（　　）
A、
1
2
B、
3
2
C、1-
3
2
D、
3
2
已知函数f（x）=sinxcosx，则f（x）是（　　）
A、奇函数
B、偶函数
C、非奇非偶函数
D、既是奇函数又是偶函数
函数f（x）=（x-2）ln（x2-4x+4）-（x-2）ln4的零点个数为（　　）
A、3B、2C、1D、0
按图所示的程序框图运算：若输出k=2，则输入x的取值范围是（　　）
A、（20，25]
B、（30，32]
C、（28，57]
D、（30，57]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网