题目内容
直线l1:x-2y+3=0,l2:2x-y-3=0,动圆C与l1、l2都相交,并且l1、l2被圆截得的线段长分别是20和16,则圆心C的轨迹方程是 .
考点:轨迹方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:设圆心C的坐标为(x,y),欲求其轨迹方程,即寻找其坐标间的关系,根据弦、弦心距、半径三者之间的关系及点到直线的距离公式即可得到.
解答:
解:设圆心C的坐标为(x,y),圆的半径为r,
点C到l1、l2的距离分别为d1,d2
根据弦、弦心距、半径三者之间的关系,有d12+102=r2,d22+82=r2,
得d22-d12=36.
根据点到直线的距离公式,得d1=
,d2=
代入上式,得方程
-
=1.
故答案为:
-
=1.
点C到l1、l2的距离分别为d1,d2
根据弦、弦心距、半径三者之间的关系,有d12+102=r2,d22+82=r2,
得d22-d12=36.
根据点到直线的距离公式,得d1=
| |x-2y+3| | ||
|
| |2x-y-3| | ||
|
代入上式,得方程
| (x-3)2 |
| 60 |
| (y-3)2 |
| 60 |
故答案为:
| (x-3)2 |
| 60 |
| (y-3)2 |
| 60 |
点评:求曲线的轨迹方程是解析几何的基本问题.求符合某种条件的动点的轨迹方程,其实质就是利用题设中的几何条件,用“坐标化”将其转化为寻求变量间的关系.

练习册系列答案
相关题目
已知如图1所示是某学生的14次数学考试成绩的茎叶图,第1次到第14次的考试成绩依次记为A1,A2,…A14,图2是统计茎叶图中成绩在一定范围内考试次数的一个程序框图,则输出的n的值是( )
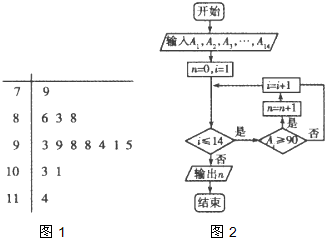

| A、8 | B、9 | C、10 | D、11 |
函数f(x)=(x-2)ln(x2-4x+4)-(x-2)ln4的零点个数为( )
| A、3 | B、2 | C、1 | D、0 |