题目内容
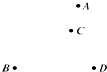如图A、B、C、D是某油田的四口油井，计划建三条路，将这四口油井连结起来（每条路只连结两口油井），那么不同的建路方案有（ ）| A、12种 | B、14种 |
| C、16种 | D、18种 |
考点：计数原理的应用
专题：
分析：由修路的方式可以分为两类：从一口井出发向其他三口井各建一条路，一口井最多建两条路，利用排列的计算公式即可得出．
解答：
解：分为以下两类：
第一类，从一口井出发向其他三口井各建一条路，共有4种方法；
第二类，一口井最多建两条路，但是象下面这样的两个排列对应一种建路方法，A-B-C-D，D-C-B-A，要去掉重复的这样，因此共有有
×4！=12种方法．
根据分类计数原理，知道共有4+12=16种．
故选C．
第一类，从一口井出发向其他三口井各建一条路，共有4种方法；
第二类，一口井最多建两条路，但是象下面这样的两个排列对应一种建路方法，A-B-C-D，D-C-B-A，要去掉重复的这样，因此共有有
| 1 |
| 2 |
根据分类计数原理，知道共有4+12=16种．
故选C．
点评：熟练掌握分类加法原理和分步乘法原理及排列的计算公式是解题的关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
已知如图1所示是某学生的14次数学考试成绩的茎叶图，第1次到第14次的考试成绩依次记为A1，A2，…A14，图2是统计茎叶图中成绩在一定范围内考试次数的一个程序框图，则输出的n的值是（ ）
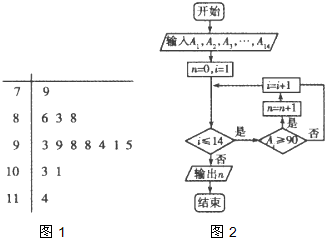
| A、8 | B、9 | C、10 | D、11 |
函数f（x）=（x-2）ln（x2-4x+4）-（x-2）ln4的零点个数为（ ）
| A、3 | B、2 | C、1 | D、0 |
给出以下命题：
①?x∈R，sinx+cosx＞1；
②?x∈R，x2-x+1＜0；
③“x＞1”是“|x|＞1”的充分不必要条件；
④若
•
=0，则|
|=|
|=0．
其中假命题的个数是（ ）
①?x∈R，sinx+cosx＞1；
②?x∈R，x2-x+1＜0；
③“x＞1”是“|x|＞1”的充分不必要条件；
④若
| a |
| b |
| a |
| b |
其中假命题的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
若z∈C且|z+2-2i|=1，则|z-1-2i|的最小值是（ ）
| A、2 | B、3 | C、4 | D、5 |
已知函数f（x）=
，则f（2）=（ ）
|
| A、3 | B、2 | C、1 | D、0 |
按图所示的程序框图运算：若输出k=2，则输入x的取值范围是（ ）
| A、（20，25] |
| B、（30，32] |
| C、（28，57] |
| D、（30，57] |