题目内容
已知函数f(x)=x|x-2|
(1)画出该函数的图象;
(2)设a>2,求f(x)在[0,a]上的最大值.
(1)画出该函数的图象;
(2)设a>2,求f(x)在[0,a]上的最大值.
考点:函数的图象
专题:函数的性质及应用
分析:(1)利用零点分段法,将函数的解析式化为分段函数的形式,进而根据二次函数的图象,得到函数f(x)=x|x-2|的图象.
(2)根据(1)中函数图象,分析a与1+
的关系,进而分类讨论可得不同情况下函数的最值.
(2)根据(1)中函数图象,分析a与1+
| 2 |
解答:
解:(1)∵f(x)=x|x-2|=
,
∴函数的图象如下图所示:
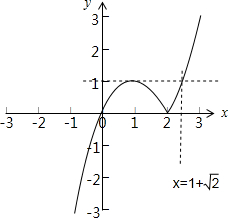
(2)当a>2时,令f(a)-f(1)=a2-2a-1=0,
解得a=1+
,或a=1-
(舍去),
当2<a<1+
时,f(a)<f(1),
此时f(x)在[0,a]上的最大值f(x)max=f(1)=1,
当a≥1+
时,f(a)≥f(1),
此时f(x)在[0,a]上的最大值f(x)max=f(a)=a2-2a.%
|
∴函数的图象如下图所示:
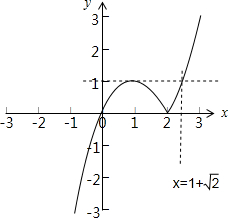
(2)当a>2时,令f(a)-f(1)=a2-2a-1=0,
解得a=1+
| 2 |
| 2 |
当2<a<1+
| 2 |
此时f(x)在[0,a]上的最大值f(x)max=f(1)=1,
当a≥1+
| 2 |
此时f(x)在[0,a]上的最大值f(x)max=f(a)=a2-2a.%
点评:本题考查的知识点是函数的图象,函数的最值,其中熟练掌握零点分段法及分段函数图象的画法,是解答的关键.

练习册系列答案
相关题目
 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.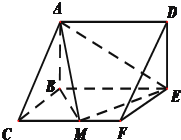 已知:直三棱柱ABC-DEF中,
已知:直三棱柱ABC-DEF中,