题目内容
在锐角△ABC中，内角A，B，C所对的边分别为a，b，c，若csinC-asinA=b（sinB-sinA），c=2．
（Ⅰ）若△ABC的面积为
，求a，b的值；
（Ⅱ）设△ABC的周长为y，试求函数y=f（A）的定义域和最大值．
（Ⅰ）若△ABC的面积为
2
| ||
| 3 |
（Ⅱ）设△ABC的周长为y，试求函数y=f（A）的定义域和最大值．
考点：正弦定理
专题：解三角形
分析：（Ⅰ）利用正弦定理和已知等式，建立a和b的关系式，进而求得cosC的值，则C的值可得，利用三角形的面积求得ab的值，最后联立方程求得a和b．
（Ⅱ）根据（Ⅰ）的C的值和c的值，分别用角的正弦表示边，相加表示出三角形的周长，利用两角和公式整理后，利用三角函数的图象和性质求得函数的定义域即最大值．
（Ⅱ）根据（Ⅰ）的C的值和c的值，分别用角的正弦表示边，相加表示出三角形的周长，利用两角和公式整理后，利用三角函数的图象和性质求得函数的定义域即最大值．
解答：
解：（Ⅰ）∵csinC-asinA=b（sinB-sinA），
∴c2-a2=b2-ab，
∴cosC=
=
，①
∴C=
，
∴S△ABC=
absinC=
ab=
，
∴ab=
，②
联立①②整理得9a4-60a2+64=0，
求得a=
，b=
或a=
，b=
．
（Ⅱ）
=
=
，
∴a=
•sinA，
同理b=
sinB，
∴y=
（sinA+sinB）+2
=
[sinA+sin（
-A）]+2
=
（
cosA+
sinA）+2=4sin（A+
）+2，
0＜A+
＜
，
∴0＜A＜
，即函数的定义域为（0，
），
当sin（A+
）=1，即A=
时，函数取最大值1，
∴y的最大值为4+2=6．
∴c2-a2=b2-ab，
∴cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
∴C=
| π |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| ||
| 4 |
2
| ||
| 3 |
∴ab=
| 8 |
| 3 |
联立①②整理得9a4-60a2+64=0，
求得a=
2
| ||
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
2
| ||
| 3 |
（Ⅱ）
| a |
| sinA |
| c |
| sinC |
4
| ||
| 3 |
∴a=
4
| ||
| 3 |
同理b=
4
| ||
| 3 |
∴y=
4
| ||
| 3 |
=
4
| ||
| 3 |
| 2π |
| 3 |
=
4
| ||
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| π |
| 6 |
0＜A+
| π |
| 6 |
| 2π |
| 3 |
∴0＜A＜
| π |
| 2 |
| π |
| 2 |
当sin（A+
| π |
| 6 |
| π |
| 3 |
∴y的最大值为4+2=6．
点评：本题主要考查了正弦定理和余弦定理的运用．解题的过程中还利用三角和公式进行三角形的恒等变换．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
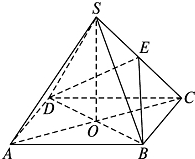如图，四棱锥S-ABCD中，底面ABCD是边长为4的正方形，O是AC与BD的交点，SO⊥平面ABCD，E是侧棱SC的中点，直线SA和AO所成角的大小是45°．
在三棱柱ABC-A1B1C1中，A1A⊥底面ABC，∠ACB=90°，AA1=AC=BC=2，D为AB中点．