题目内容
 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.(1)求二面角B1-BD-A1的余弦值;
(2)求点C1到平面A1BD的距离.
考点:二面角的平面角及求法,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(1)取BC中点O,连结AO,由已知条件得AO⊥BC,平面ABC⊥平面BCC1B1,以O为原点,
,
,
的方向为x,y,z轴的正方向,建立空间直角坐标系,利用向量法能求出二面角B1-BD-A1的余弦值.
(2)由
=(1,2,-
)为平面A1BD的法向量,
=(0,1,0),利用向量法能求出C1点到A1BD的距.
| OB |
| OO1 |
| OA |
(2)由
| AB1 |
| 3 |
| DC1 |
解答:
解:(1)取BC中点O,连结AO,
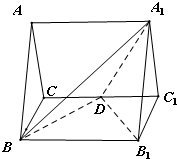 ∵△ABC为正三角形,∴AO⊥BC.
∵△ABC为正三角形,∴AO⊥BC.
∵在正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,
∴AO⊥平面BCC1B1.
取B1C1中点O1,以O为原点,
,
,
的方向为x,y,z轴的正方向,
建立空间直角坐标系,
则B(1,0,0),D(-1,1,0),A1(0,2,
),
A(0,0,
),B1(1,2,0),C1(-1,2,0)
∴
=(1,2,-
),
=(-2,1,0),
=(-1,2,
).
∴
•
=0,
•
=0
∴
⊥
,
⊥
,∴AB1⊥平面BDA1.
即
=(1,2,-
)为平面BDA1的法向量.
取平面B1BD的一个法向量为
=(0 ,0 ,
),
cos<
,
>=
=
=-
.
∴二面角B1-BD-A1的余弦值为
.
(2)∵
=(1,2,-
)为平面A1BD的法向量,
=(0,1,0)
∴C1点到平面A1BD的距离为:
d=|
|=|
|=
=
.
 ∵△ABC为正三角形,∴AO⊥BC.
∵△ABC为正三角形,∴AO⊥BC.∵在正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,
∴AO⊥平面BCC1B1.
取B1C1中点O1,以O为原点,
| OB |
| OO1 |
| OA |
建立空间直角坐标系,
则B(1,0,0),D(-1,1,0),A1(0,2,
| 3 |
A(0,0,
| 3 |
∴
| AB1 |
| 3 |
| BD |
| BA1 |
| 3 |
∴
| AB1 |
| BD |
| AB1 |
| BA1 |
∴
| AB1 |
| BD |
| AB1 |
| BA1 |
即
| AB1 |
| 3 |
取平面B1BD的一个法向量为
| n |
| 3 |
cos<
| n |
| AB1 |
| ||||
|
| -3 | ||||
2
|
| ||
| 4 |
∴二面角B1-BD-A1的余弦值为
| ||
| 4 |
(2)∵
| AB1 |
| 3 |
| DC1 |
∴C1点到平面A1BD的距离为:
d=|
| ||||
| |AB1| |
(0,1,0)•(1,2,-
| ||
|
| 2 | ||
2
|
| ||
| 2 |
点评:本题考查二面角的余弦值的求法,考查点到平面的距离的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知双曲线
-
=1的一条渐近线方程为4x+3y=0,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=4,AD=2,PA=2,PD=
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=4,AD=2,PA=2,PD= 如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.
如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.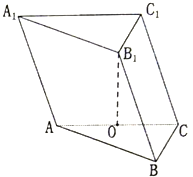 已知三棱柱ABC-A1B1C1的各条棱长均为2,点B1在平面ABC内的射影恰好落在AC边的中点O处.
已知三棱柱ABC-A1B1C1的各条棱长均为2,点B1在平面ABC内的射影恰好落在AC边的中点O处.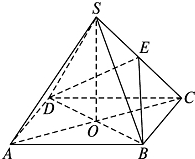 如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,O是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,直线SA和AO所成角的大小是45°.
如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,O是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,直线SA和AO所成角的大小是45°.