题目内容
已知向量
=(-3,4),|
|=2,
和
的夹角是60°.
(1)求
•
的值;
(2)求|
-2
|.
| a |
| b |
| a |
| b |
(1)求
| a |
| b |
(2)求|
| a |
| b |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:(1)先求出向量
的模,然后代入向量的数量积公式;(2)先求模长的平方,这样就转化成了向量的数量积运算,然后再开方.
| a |
解答:
解:(1)∵向量
=(-3,4),
∴|
|=
=5
∴
•
=|
|•|
|cos60°
=5×2×
=5.
(2)∵|
-2
|2=
2+4
2-4
•
=25+4-4×5=9
∴|
-2
|=3.
| a |
∴|
| a |
| (-3)2+42 |
∴
| a |
| b |
| a |
| b |
=5×2×
| 1 |
| 2 |
(2)∵|
| a |
| b |
| a |
| b |
| a |
| b |
=25+4-4×5=9
∴|
| a |
| b |
点评:本题考查了向量的数量积及向量的模长,求向量的模长时一般先通过平方转化成向量的数量积运算.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
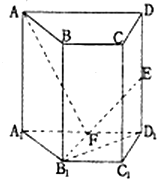 如图,四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,AD⊥DC,AD∥BC,AD=DD1=2,BC=DC=1.点E是侧棱DD1的中点.
如图,四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,AD⊥DC,AD∥BC,AD=DD1=2,BC=DC=1.点E是侧棱DD1的中点.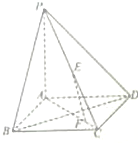 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E是PC中点,F为线段AC上一点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E是PC中点,F为线段AC上一点.