题目内容
已知椭圆C:
+
=1(a>b>0)经过点M(1,
),其离心率为
,经过点(0,
),斜率为k的直线l与椭圆C相交于P、Q两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)求k的取值范围;
(Ⅲ)设椭圆C与x轴正半轴、y轴正半轴分别相交于A、B两点,则是否存在常数k,使得向量
+
与
共线?如果存在,求k值;如果不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)求k的取值范围;
(Ⅲ)设椭圆C与x轴正半轴、y轴正半轴分别相交于A、B两点,则是否存在常数k,使得向量
| OP |
| OQ |
| AB |
考点:直线与圆锥曲线的综合问题
专题:计算题,向量与圆锥曲线,圆锥曲线中的最值与范围问题
分析:(Ⅰ)由题意,e=
=
,a2=b2+c2,并将点M代入可求出椭圆C的方程;
(Ⅱ)由题意,联立方程化简可得(
+k2)x2+2
kx+1=0,则△=8k2-4(
+k2)=4k2-2>0,从而求k的取值范围;
(Ⅲ)假设存在,设P(x1,y1),Q(x2,y2),则
+
=(x1+x2,y1+y2),
=(-
,1);由向量
+
与
共线可得x1+x2=-
(y1+y2),利用韦达定理可解得k=
,结合(Ⅱ)知不存在.
| c |
| a |
| ||
| 2 |
(Ⅱ)由题意,联立方程化简可得(
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
(Ⅲ)假设存在,设P(x1,y1),Q(x2,y2),则
| OP |
| OQ |
| AB |
| 2 |
| OP |
| OQ |
| AB |
| 2 |
| ||
| 2 |
解答:
解:(Ⅰ)由题意,e=
=
,
又∵a2=b2+c2,
∴a2=2b2,
∴椭圆C的方程为
+
=1,
将点M(1,
)代入,得b2=1,a2=2,
∴所求椭圆方程为
+y2=1.
(Ⅱ)由已知条件,直线l的方程为y=kx+
,
代入椭圆方程得
+(kx+
)2=1.
整理得(
+k2)x2+2
kx+1=0①,
直线l与椭圆有两个不同的交点P和Q等价于
△=8k2-4(
+k2)=4k2-2>0,
解得,k<-
或k>
.
即k的取值范围为(-∞,-
)∪(
,+∞).
(Ⅲ)设P(x1,y1),Q(x2,y2),则
+
=(x1+x2,y1+y2),
由方程①得,x1+x2=-
②,
又y1+y2=k(x1+x2)+2
③,
而A(
,0),B(0,1),
=(-
,1);
又∵
+
与
共线,
∴x1+x2=-
(y1+y2),
将②③代入上式解得,k=
.
由(Ⅱ)知,k<-
或k>
,
故没有符合题意的常数k.
| c |
| a |
| ||
| 2 |
又∵a2=b2+c2,
∴a2=2b2,
∴椭圆C的方程为
| x2 |
| 2b2 |
| y2 |
| b2 |
将点M(1,
| ||
| 2 |
∴所求椭圆方程为
| x2 |
| 2 |
(Ⅱ)由已知条件,直线l的方程为y=kx+
| 2 |
代入椭圆方程得
| x2 |
| 2 |
| 2 |
整理得(
| 1 |
| 2 |
| 2 |
直线l与椭圆有两个不同的交点P和Q等价于
△=8k2-4(
| 1 |
| 2 |
解得,k<-
| ||
| 2 |
| ||
| 2 |
即k的取值范围为(-∞,-
| ||
| 2 |
| ||
| 2 |
(Ⅲ)设P(x1,y1),Q(x2,y2),则
| OP |
| OQ |
由方程①得,x1+x2=-
4
| ||
| 1+2k2 |
又y1+y2=k(x1+x2)+2
| 2 |
而A(
| 2 |
| AB |
| 2 |
又∵
| OP |
| OQ |
| AB |
∴x1+x2=-
| 2 |
将②③代入上式解得,k=
| ||
| 2 |
由(Ⅱ)知,k<-
| ||
| 2 |
| ||
| 2 |
故没有符合题意的常数k.
点评:本题考查了椭圆方程的求法,同时考查了椭圆与直线的综合问题,常利用韦达定理简化运算,同时考查了向量的应用,属于难题.

练习册系列答案
相关题目
函数f(x)=
的定义域是( )
| 1 |
| log3(x-2) |
| A、(-∞,2) |
| B、(2,+∞) |
| C、(2,3)∪(3,+∞) |
| D、(2,5)∪(5,+∞) |
已知直线l1的方向向量
=(1.1,1),直线l2的方向向量
=(-2.2,-2),则l1,l2夹角的余弦值为( )
| s1 |
| s2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,平面PAD⊥平面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为PA的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,平面PAD⊥平面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为PA的中点.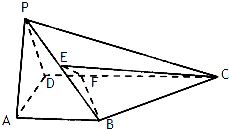 如图,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,△PAD是边长为
如图,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,△PAD是边长为