题目内容
如图所示，在⊙O上半圆中，AC=a，CB=b，CD⊥AB，EO⊥AB，请你利用CD≤OD≤CE写出一个含有a，b的不等式考点：基本不等式
专题：不等式的解法及应用
分析：连接AD，BD，OD，根据直角三角形的斜边上的中线等于斜边的一半，求出OD，在直角三角形ABD中，应用角的正切定义求出CD，根据CD≤OD从而得到
≤
，在直角三角形EOC中，由勾股定理得到EC=
，又EO=OD≤EC，从而
≤
．
| ab |
| a+b |
| 2 |
|
| a+b |
| 2 |
|
解答：
解：连接AD，BD，OD，由直径所对的圆周角为直角得，∠ADB=90°，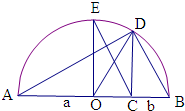
∵AC=a，CB=b，∴OD=
=
，
在直角三角形DAC中，tan∠DAC=
=
，
在直角三角形BCD中，tan∠DBC=
=
，
又∠DAC+∠DBC=90°，
∴
•
=1，CD=
，
由于CD≤OD，故
≤
，
∵EO⊥AB，EO=
，
∴EC=
=
=
又EO=OD≤EC，
∴
≤
，
∴
≤
≤
．
故答案为：
≤
≤
．
∵AC=a，CB=b，∴OD=
| AB |
| 2 |
| a+b |
| 2 |
在直角三角形DAC中，tan∠DAC=
| CD |
| AC |
| CD |
| a |
在直角三角形BCD中，tan∠DBC=
| CD |
| BC |
| CD |
| b |
又∠DAC+∠DBC=90°，
∴
| CD |
| a |
| CD |
| b |
| ab |
由于CD≤OD，故
| ab |
| a+b |
| 2 |
∵EO⊥AB，EO=
| a+b |
| 2 |
∴EC=
| EO2+OC2 |
|
|
又EO=OD≤EC，
∴
| a+b |
| 2 |
|
∴
| ab |
| a+b |
| 2 |
|
故答案为：
| ab |
| a+b |
| 2 |
|
点评：本题主要考查基本不等式的几何证明，考查平面几何的基础知识：直角三角形的勾股定理、斜边上的中线等于斜边的一半，以及三角函数的定义等，是一道基础题．
练习册系列答案
相关题目
在矩形ABCD中，AB=2，AD=3，AB中点为E，点F，G分别在线段AD，BC上随机运动，则∠FEG为锐角的概率是