题目内容
已知{an}是各项都为正数的等比数列，Sn是其前n项和，若a1=1，5S2=S4，则a5= ．
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：分析等比数列公比不等于1，设出等比数列的公比，由给出的条件列方程组求出a1和q的值，则a5的值可求．
解答：
解：若等比数列的公比等于1，由a1=1，则S4=4，5S2=10，与题意不符．
设等比数列的公比为q（q≠1），
由a1=1，5S2=S4，得：5•
=
，
解得q=±2．
因为数列{an}的各项均为正数，所以q=2．
则a5=a1q4=16．
故答案为：16．
设等比数列的公比为q（q≠1），
由a1=1，5S2=S4，得：5•
| 1-q2 |
| 1-q |
| 1-q4 |
| 1-q |
解得q=±2．
因为数列{an}的各项均为正数，所以q=2．
则a5=a1q4=16．
故答案为：16．
点评：本题考查了等比数列的前n项和，考查了分类讨论过的数学思想，在利用等比数列的前n项和公式时，一定要注意对公比的讨论，此题是基础题．
练习册系列答案
相关题目
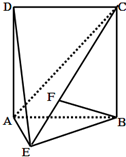如图，直二面角D-AB-E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE．
如图所示，在⊙O上半圆中，AC=a，CB=b，CD⊥AB，EO⊥AB，请你利用CD≤OD≤CE写出一个含有a，b的不等式