题目内容
“p：x∈{x|x2-x-2≥0}”，“q：x∈{x|x＜a}”，若￢p是q的充分不必要条件，则a的取值范围是 ．
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：求出p的等价条件，利用充分不必要条件的定义建立，建立条件关系即可求实数a的取值范围．
解答：
解：由x2-x-2≥0得x≥2或x≤-1，即p：x≥2或x≤-1，￢p：-1＜x＜2．
若￢p是q的充分不必要条件，
则{x|-1＜x＜2}?{x|x＜a}，
即a≥2，
故答案为：a≥2．
若￢p是q的充分不必要条件，
则{x|-1＜x＜2}?{x|x＜a}，
即a≥2，
故答案为：a≥2．
点评：本题主要考查充分条件和必要条件的应用，考查学生的推理能力．利用不等式的性质是解决本题的关键．
练习册系列答案
相关题目
如图所示，在⊙O上半圆中，AC=a，CB=b，CD⊥AB，EO⊥AB，请你利用CD≤OD≤CE写出一个含有a，b的不等式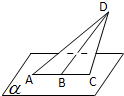
平面ACD⊥平面α，B为AC的中点，AC=2，∠CBD=60°，P是α内的动点，且P到直线BD的距离为