题目内容
 在矩形ABCD中,AB=2,AD=3,AB中点为E,点F,G分别在线段AD,BC上随机运动,则∠FEG为锐角的概率是
在矩形ABCD中,AB=2,AD=3,AB中点为E,点F,G分别在线段AD,BC上随机运动,则∠FEG为锐角的概率是考点:几何概型
专题:概率与统计
分析:利用两角和的正切公式,利用线性规划,以及几何概型的概率公式即可得到结论.
解答:
解:设FA=x,GB=y,
则0≤x≤3,0≤y≤3,平面区域{(x,y)|0≤x≤3,0≤y≤3}对应的区域是正方形边长为3,面积S=9.
则tan∠FEA=
=x,tan∠GEB=
=y,
则tan(∠GEB+∠FEA)=
=
,
若∠FEG为锐角,则等价为∠GEB+∠FEA是钝角,
即tan(∠GEB+∠FEA)=
<0,
即1-xy<0,即y>
,
作出对应的平面区域如图:
当y=3时,由
=3,解得x=
,A(
,3),
当x=3时,y=
,即B(3,
),
则矩形ODAE的面积S=3×
=1,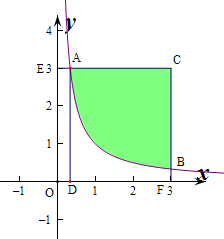
曲边四边形ACFB的面积S=
dx═lnx|
=ln3-ln
=2ln3,
∴阴影部分的面积S=9-1-2ln3=8-2ln3,
(阴影部分的面积也可以这样求S=
(3-
)dx=(3x-lnx)
=8-2ln3,)
∴根据几何概型的概率公式可得∠FEG为锐角的概率
,
故答案为:
则0≤x≤3,0≤y≤3,平面区域{(x,y)|0≤x≤3,0≤y≤3}对应的区域是正方形边长为3,面积S=9.
则tan∠FEA=
| AF |
| AE |
| BG |
| BE |
则tan(∠GEB+∠FEA)=
| tan∠FEA+tan∠GEB |
| 1-tan∠FEA•tan∠GEB |
| x+y |
| 1-xy |
若∠FEG为锐角,则等价为∠GEB+∠FEA是钝角,
即tan(∠GEB+∠FEA)=
| x+y |
| 1-xy |
即1-xy<0,即y>
| 1 |
| x |
作出对应的平面区域如图:
当y=3时,由
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
当x=3时,y=
| 1 |
| 3 |
| 1 |
| 3 |
则矩形ODAE的面积S=3×
| 1 |
| 3 |

曲边四边形ACFB的面积S=
| ∫ | 3
|
| 1 |
| x |
3
|
| 1 |
| 3 |
∴阴影部分的面积S=9-1-2ln3=8-2ln3,
(阴影部分的面积也可以这样求S=
| ∫ | 3
|
| 1 |
| x |
| | | 3
|
∴根据几何概型的概率公式可得∠FEG为锐角的概率
| 8-2ln3 |
| 9 |
故答案为:
| 8-2ln3 |
| 9 |
点评:本题主要考查几何概型的概率计算,根据条件将∠FEG为锐角进行转化,利用积分求出对应区域的面积是解决本题的关键,综合性较强,涉及的知识点较多.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
如图是某算法的程序框图,则程序运行后输出的结果是( )

| A、8 | B、9 | C、10 | D、11 |
 如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,EO⊥AB,请你利用CD≤OD≤CE写出一个含有a,b的不等式
如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,EO⊥AB,请你利用CD≤OD≤CE写出一个含有a,b的不等式